|
In 1838, G. B. Airy investigated the simple-looking differential equation:
This is quite similar to the differential equation 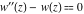 for the hyperbolic sine and hyperbolic cosine functions, which has the general solution for the hyperbolic sine and hyperbolic cosine functions, which has the general solution 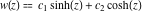 . Airy built two partial solutions . Airy built two partial solutions 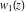 and and 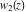 for the first equation in the form of a power series for the first equation in the form of a power series 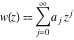 . These solutions were named the Airy functions. Much later, H. Jeffreys (1928–1942) investigated these functions more deeply. The current notations Ai and Bi were proposed by J. C. P. Miller (1946). . These solutions were named the Airy functions. Much later, H. Jeffreys (1928–1942) investigated these functions more deeply. The current notations Ai and Bi were proposed by J. C. P. Miller (1946).
The Airy functions 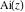 and and 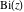 are the special solutions of the differential equation: are the special solutions of the differential equation:
satisfying the following initial conditions:
These functions have different equivalent representations in the form of series or generalized hypergeometric functions. The hypergeometric representation can be conveniently used as a definition of the Airy functions.
|