|
The Bessel functions 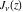 , , 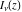 , , 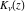 , and , and 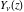 are particular cases of more general functions: hypergeometric and Meijer G functions. are particular cases of more general functions: hypergeometric and Meijer G functions.
In particular, the functions 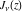 and and 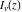 can be represented through the regularized hypergeometric functions can be represented through the regularized hypergeometric functions 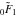 (without any restrictions on the parameter (without any restrictions on the parameter 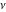 ): ):
Similar formulas, but with restrictions on the parameter 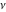 , represent , represent 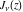 and and 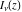 through the classical hypergeometric function through the classical hypergeometric function 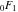 : :
The functions 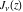 and and 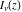 can also be represented through the hypergeometric functions can also be represented through the hypergeometric functions 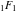 by the following formulas: by the following formulas:
Similar formulas for other Bessel functions 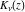 and and 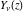 always include restrictions on the parameter, namely always include restrictions on the parameter, namely 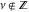 : :
In the case of integer 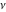 , the right‐hand sides of the preceding six formulas evaluate to removable indeterminate expressions of the type , the right‐hand sides of the preceding six formulas evaluate to removable indeterminate expressions of the type 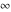 , , 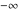 . The limit of the right‐hand sides exists and produces complicated series expansions including logarithmic and polygamma functions. These difficulties can be removed by using the generalized Meijer G function. The generalized Meijer G function allows represention of all four Bessel functions for all values of the parameter . The limit of the right‐hand sides exists and produces complicated series expansions including logarithmic and polygamma functions. These difficulties can be removed by using the generalized Meijer G function. The generalized Meijer G function allows represention of all four Bessel functions for all values of the parameter 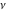 by the following simple formulas: by the following simple formulas:
The classical Meijer G function is less convenient because it can lead to additional restrictions:
Each of the Bessel functions can be represented through other Bessel functions:
|