|
Definitions of Bessel functions
The Bessel functions of the first kind 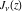 and and 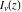 are defined as sums of the following infinite series: are defined as sums of the following infinite series:
These sums are convergent everywhere in the complex 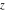 ‐plane. The Bessel functions of the second kind ‐plane. The Bessel functions of the second kind 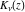 and and 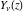 for noninteger parameter for noninteger parameter 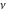 are defined as special linear combinations of the last two functions: are defined as special linear combinations of the last two functions:
In the case of integer index 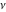 , the right‐hand sides of the previous expressions give removable indeterminate values of the type , the right‐hand sides of the previous expressions give removable indeterminate values of the type 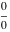 . In this case, the Bessel functions . In this case, the Bessel functions  and and 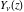 are defined through the following limits: are defined through the following limits:
|