|
The Struve functions 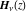 and and 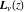 appeared as special solutions of the inhomogeneous Bessel second-order differential equations: appeared as special solutions of the inhomogeneous Bessel second-order differential equations:
where 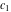 and and 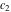 are arbitrary constants and are arbitrary constants and  , , 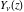 , ,  , and , and 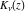 are Bessel functions. are Bessel functions.
The last two differential equations are very similar and can be converted into each other by changing 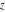 to to 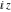 . Their solutions can be constructed in the form of a series with arbitrary coefficients: . Their solutions can be constructed in the form of a series with arbitrary coefficients:
Substitution of this series into the first equation gives the following partial solution of the inhomogeneous equation:
This solution, which appeared in an article by H. Struve (1882), was later ascribed Struve's name and the special notation 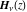 . .
A similar procedure carried out for the second inhomogeneous equation leads to the function 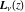 , which was introduced by J. W. Nicholson (1911). , which was introduced by J. W. Nicholson (1911).
|