|
Introduction to the Struve functions
General
The Struve functions 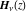 and and 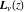 appeared as special solutions of the inhomogeneous Bessel second-order differential equations: appeared as special solutions of the inhomogeneous Bessel second-order differential equations:
where 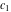 and and 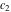 are arbitrary constants and are arbitrary constants and  , , 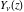 , ,  , and , and 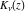 are Bessel functions. are Bessel functions.
The last two differential equations are very similar and can be converted into each other by changing 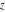 to to 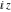 . Their solutions can be constructed in the form of a series with arbitrary coefficients: . Their solutions can be constructed in the form of a series with arbitrary coefficients:
Substitution of this series into the first equation gives the following partial solution of the inhomogeneous equation:
This solution, which appeared in an article by H. Struve (1882), was later ascribed Struve's name and the special notation 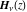 . .
A similar procedure carried out for the second inhomogeneous equation leads to the function 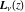 , which was introduced by J. W. Nicholson (1911). , which was introduced by J. W. Nicholson (1911).
Definitions of Struve functions
The Struve functions 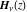 and and  are defined as sums of the following infinite series: are defined as sums of the following infinite series:
A quick look at the Struve functions Here is a quick look at the graphics for the Struve functions along the real axis.
Connections within the group of Struve functions and with other function groups
Representations through more general functions
The Struve functions  and and 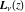 are particular cases of the more general hypergeometric and Meijer G functions. are particular cases of the more general hypergeometric and Meijer G functions.
For example, they can be represented through regularized hypergeometric functions 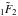 : :
In the cases when 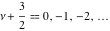 , the previous formulas degenerate into the following: , the previous formulas degenerate into the following:
For general values of parameter 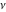 , the Struve functions , the Struve functions 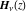 and and 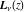 cannot be represented through classical hypergeometric functions without restrictions on parameter cannot be represented through classical hypergeometric functions without restrictions on parameter 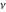 : :
Similar conclusion can be drawn from the following representations of the Struve functions 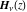 and and 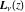 through generalized and classical Meijer G functions: through generalized and classical Meijer G functions:
The first two formulas are simpler than the last two classical representations that include factors like 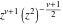 . .
Transformation inside the group (Interconnections)
The Struve functions 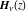 and and 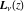 are connected to each other by the formulas: are connected to each other by the formulas:
The best-known properties and formulas for Struve functions
Real values for real arguments
For real values of parameter 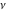 and positive argument and positive argument 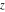 , the values of the Struve functions , the values of the Struve functions 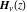 and and  are real. are real.
Simple values at zero
The Struve functions  and and 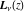 have rather simple values for the argument have rather simple values for the argument 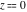 : :
Specific values for specialized parameter
In the cases when parameter 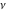 is equal to is equal to 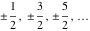 , the Struve functions , the Struve functions 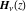 and and 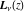 can be expressed through the sine and cosine (or hyperbolic sine and cosine) multiplied by rational and sqrt functions, for example: can be expressed through the sine and cosine (or hyperbolic sine and cosine) multiplied by rational and sqrt functions, for example:
The previous formulas are the particular cases of the following general formulas:
Analyticity
The Struve functions 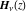 and and 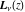 are defined for all complex values of their parameter are defined for all complex values of their parameter 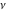 and variable and variable 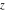 . They are analytical functions of . They are analytical functions of 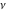 and and  over the whole complex over the whole complex 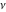 ‐ and ‐ and  ‐planes excluding the branch cuts. For fixed integer ‐planes excluding the branch cuts. For fixed integer 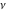 , the functions , the functions 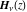 and and 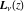 are entire functions of are entire functions of  . For fixed . For fixed 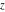 , the functions , the functions 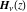 and and 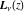 are entire functions of are entire functions of 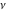 . .
Poles and essential singularities
For fixed 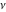 , the functions , the functions 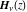 and and 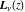 have an essential singularity at have an essential singularity at 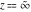 . At the same time, the point . At the same time, the point 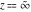 is a branch point (except cases for integer is a branch point (except cases for integer 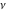 ). ).
With respect to 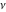 , the Struve functions have only one essential singular point at , the Struve functions have only one essential singular point at 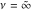 . .
Branch points and branch cuts.
For fixed noninteger 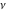 , the functions , the functions 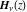 and and 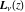 have two branch points: have two branch points: 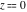 and and 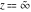 . .
If functions 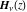 and and 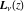 have branch cuts, they are single‐valued functions on the have branch cuts, they are single‐valued functions on the 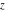 ‐plane cut along the interval ‐plane cut along the interval  , where they are continuous from above: , where they are continuous from above:
From below, functions have discontinuities that are described by the formulas:
Periodicity
The Struve functions 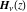 and and 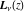 do not have periodicity. do not have periodicity.
Parity and symmetry
The Struve functions 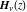 and and 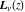 have mirror symmetry (except on the branch cut interval (-∞, 0)): have mirror symmetry (except on the branch cut interval (-∞, 0)):
The Struve functions 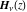 and and 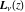 have generalized parity (either odd or even) with respect to variable have generalized parity (either odd or even) with respect to variable 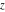 : :
Series representations
The Struve functions  and and 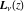 have the following series expansions through series that converge on the whole have the following series expansions through series that converge on the whole  ‐plane: ‐plane:
Interestingly, closed-form expressions for the truncated version of the Taylor series at the origin can be expressed through the generalized hypergeometric function 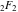 , for example: , for example:
Asymptotic series expansions
The asymptotic behavior of the Struve functions 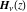 and and  can be described by the following formulas (only the main terms of asymptotic expansion are given): can be described by the following formulas (only the main terms of asymptotic expansion are given):
The previous formulas are valid in any directions approaching point 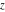 to infinity (z∞). In particular cases when to infinity (z∞). In particular cases when 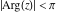 or or 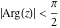 , these formulas can be simplified to the following relations: , these formulas can be simplified to the following relations:
Integral representations
The Struve functions 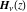 and and 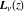 have simple integral representations through the sine (or hyperbolic sine) and power functions: have simple integral representations through the sine (or hyperbolic sine) and power functions:
Transformations
Arguments of the Struve functions 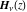 and and 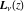 with square root arguments can sometimes be simplified: with square root arguments can sometimes be simplified:
Identities
The Struve functions  and and 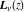 satisfy the following recurrence identities: satisfy the following recurrence identities:
The previous identities can be generalized to the following recurrence identities with a jump of length n:
Simple representations of derivatives
The derivatives of the Struve functions 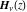 and and 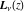 have simple representations that can also be expressed through Struve functions with different indices: have simple representations that can also be expressed through Struve functions with different indices:
The symbolic 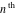 -order derivatives have the following representations: -order derivatives have the following representations:
Differential equations
The Struve functions 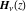 and and 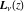 appeared as special solutions of the special inhomogeneous Bessel second-order linear differential equations: appeared as special solutions of the special inhomogeneous Bessel second-order linear differential equations:
where 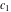 and and 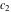 are arbitrary constants and are arbitrary constants and 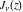 , , 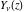 , , 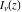 , and , and  are Bessel functions.
The previous equations are very similar and can be converted into each other by changing are Bessel functions.
The previous equations are very similar and can be converted into each other by changing 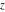 to to 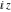 . .
Applications of Struve functions
Applications of Struve functions include electrodynamics, potential theory, and optics.
|