|
General
The study of complex numbers and their characteristics has a long history. It all started with questions about how to understand and interpret the solution of the simple quadratic equation 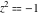 . .
It was clear that 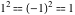 . But it was not clear how to get –1 from something squared. . But it was not clear how to get –1 from something squared.
This problem was intensively discussed in the 16th, 17th, and 18th centuries. As a result, mathematicians proposed a special symbol—the imaginary unit 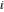 , which is represented by , which is represented by 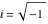 : :
L. Euler (1755) introduced the word "complex" (1777) and first used the letter 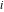 for denoting for denoting  . Later, C. F. Gauss (1831) introduced the name "imaginary unit" for . Later, C. F. Gauss (1831) introduced the name "imaginary unit" for 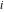 . .
Accordingly, 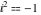 and and 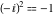 and the above quadratic equation has two solutions as is expected for a quadratic polynomial: and the above quadratic equation has two solutions as is expected for a quadratic polynomial:
The imaginary unit 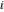 was interpreted in a geometrical sense as the point with coordinates was interpreted in a geometrical sense as the point with coordinates  in the Cartesian (Euclidean) in the Cartesian (Euclidean)  , ,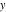 ‐plane with the vertical ‐plane with the vertical 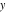 -axis upward and the origin -axis upward and the origin 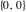 . This geometric interpretation established the following representations of the complex number . This geometric interpretation established the following representations of the complex number 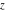 through two real numbers through two real numbers 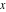 and and 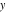 as: as:
where 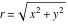 is the distance between points is the distance between points 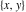 and and  , and , and 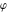 is the angle between the line connecting the points is the angle between the line connecting the points 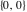 and and 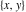 and the positive and the positive  -axis direction (the so-called polar representation). -axis direction (the so-called polar representation).
The last formula lead to the basic relations:
which describe the main characteristics of the complex number  —the so-called modulus (absolute value) —the so-called modulus (absolute value) 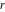 , the real part , the real part 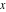 , the imaginary part , the imaginary part 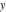 , and the argument , and the argument  . .
A new era in the theory of complex numbers and functions of complex arguments (analytic functions) arose from the investigations of L. Euler (1727, 1728). In a letter to Goldbach (1731) L. Euler introduced the notation ⅇ for the base of the natural logarithm ⅇ⩵2.71828182…, and he proved that ⅇ is irrational. Later on L. Euler (1740–1748) found a series expansion for 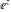 , which lead to the famous very basic formula, connecting exponential and trigonometric functions: , which lead to the famous very basic formula, connecting exponential and trigonometric functions:
This is known as the Euler formula (although it was already derived by R. Cotes in 1714).
The Euler formula allows presentation of the complex number 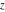 , using polar coordinates , using polar coordinates  in the more compact form: in the more compact form:
It also expressed the logarithm of complex numbers through the formula:
Taking into account that the cosine and sine have period 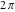 , it follows that , it follows that 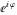 has period has period 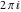 : :
Generically, the logarithm function 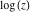 is the multivalued function: is the multivalued function:
For specifying just one value for the logarithm 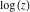 and one value of the argument φ for a given complex number and one value of the argument φ for a given complex number 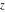 , the restriction , the restriction 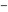 π < φ ≤ π for the argument φ is generally used. π < φ ≤ π for the argument φ is generally used.
During the 18th and 19th centuries many mathematicians worked on building the theory of the functions of complex variables, which was called the theory of analytic functions. Today this is a widely used theory, not only for the above‐mentioned four complex components (absolute value, argument, real and imaginary parts), but for complimentary characteristics of a complex number 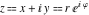 such as the conjugate complex number such as the conjugate complex number 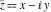 and the signum (sign) and the signum (sign) 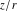 . J. R. Argand (1806, 1814) introduced the word "module" for the absolute value, and A. L. Cauchy (1821) was the first to use the word "conjugate" for complex numbers in the modern sense. Later K. Weierstrass (1841) introduced the notation ❘z❘ for the absolute value. . J. R. Argand (1806, 1814) introduced the word "module" for the absolute value, and A. L. Cauchy (1821) was the first to use the word "conjugate" for complex numbers in the modern sense. Later K. Weierstrass (1841) introduced the notation ❘z❘ for the absolute value.
It was shown that the set of complex numbers and the set of real numbers have basic properties in common—they both are fields because they satisfy so-called field axioms. Complex and real numbers exhibit commutativity under addition and multiplication described by the formulas:
Complex and real numbers also have associativity under addition and multiplication described by the formulas:
and distributivity described by the formulas:
(The set of rational numbers 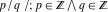 also satisfies all of the previous field axioms and is also a field. This set is countable, which means that each rational number can be numerated and placed in a definite position with a corresponding integer number also satisfies all of the previous field axioms and is also a field. This set is countable, which means that each rational number can be numerated and placed in a definite position with a corresponding integer number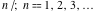 . But the set of rational numbers does not include so-called irrational numbers like . But the set of rational numbers does not include so-called irrational numbers like 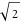 or or 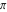 . The set of irrational numbers is much larger and cannot be numerated. The sets of all real and complex numbers form uncountable sets.) . The set of irrational numbers is much larger and cannot be numerated. The sets of all real and complex numbers form uncountable sets.)
The great success and achievements of the complex number theory stimulated attempts to introduce not only the imaginary unit 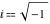 in the Cartesian (Euclidean) plane in the Cartesian (Euclidean) plane 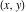 , but a similar special third unit , but a similar special third unit 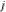 in Cartesian (Euclidean) three-dimensional space in Cartesian (Euclidean) three-dimensional space 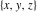 , which can be used for building a similar theory of (hyper)complex numbers , which can be used for building a similar theory of (hyper)complex numbers 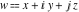 : :
Unfortunately, such an attempt fails to fulfill the field axioms. Further generalizations to build the so‐called quaternions and octonions are needed to obtain mathematically interesting and rich objects.
|