|
For real values of argument  , the values of all six complex components , the values of all six complex components 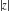 , , 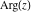 , , 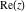 , , 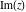 , , 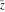 , and , and 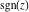 are real. are real.
The six complex components 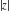 , , 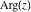 , , 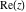 , , 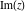 , , 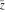 , and , and 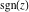 have the following values for the argument have the following values for the argument 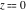 : :
 is not a uniquely defined number. Depending on the argument of is not a uniquely defined number. Depending on the argument of 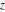 , the limit , the limit 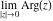 can take any value in the interval can take any value in the interval 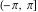 . .
The six complex components 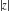 , , 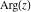 , , 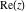 , , 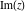 , ,  , and , and 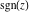 have the following values for some concrete numeric arguments: have the following values for some concrete numeric arguments:
Restricted arguments have the following formulas for the six complex components 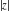 , , 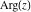 , , 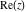 , , 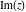 , , 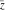 , and , and  : :
The values of complex components 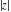 , , 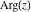 , , 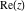 , , 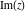 , , 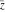 , and , and 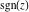 at any infinity can be described through the following: at any infinity can be described through the following:
All six complex components  , , 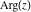 , ,  , , 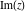 , ,  , and , and 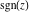 are not analytical functions. None of them fulfills the Cauchy–Riemann conditions and as such the value of the derivative depends on the direction. The functions are not analytical functions. None of them fulfills the Cauchy–Riemann conditions and as such the value of the derivative depends on the direction. The functions 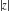 , , 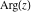 , , 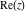 , and , and 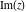 are real‐analytic functions of the variable are real‐analytic functions of the variable  (except, maybe, (except, maybe, 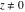 ). The real and the imaginary parts of ). The real and the imaginary parts of 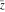 and and 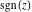 are real‐analytic functions of the variable are real‐analytic functions of the variable  . .
The four complex components 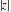 , , 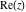 , , 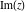 , and , and 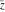 are continuous functions in are continuous functions in 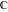 .
The function .
The function  has discontinuity at point has discontinuity at point 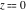 . .
The function 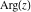 is a single‐valued, continuous function on the is a single‐valued, continuous function on the 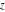 ‐plane cut along the interval ‐plane cut along the interval 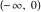 , where it is continuous from above. Its behavior can be described by the following formulas: , where it is continuous from above. Its behavior can be described by the following formulas:
All six complex components  , , 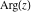 , ,  , , 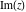 , , 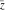 , and , and  do not have any periodicity. do not have any periodicity.
All six complex components 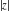 , ,  , , 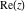 , ,  , , 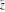 , and , and 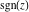 have mirror symmetry: have mirror symmetry:
The absolute value 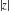 is an even function. The four complex components is an even function. The four complex components 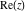 , , 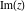 , , 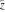 , and , and 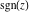 are odd functions. The argument are odd functions. The argument 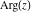 is an odd function for almost all is an odd function for almost all 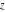 : :
The six complex components 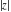 , , 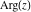 , , 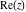 , , 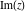 , , 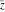 , and , and 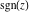 have the following homogeneity properties: have the following homogeneity properties:
Some complex components have scale symmetry:
The functions 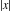 and and 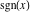 with real with real 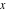 have the following series expansions near point have the following series expansions near point 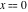 : :
The function 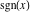 with real with real 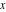 has the following contour integral representation: has the following contour integral representation:
The functions 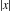 and and 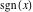 with real with real 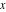 have the following limit representations: have the following limit representations:
The last two representations are sometimes called generalized Padé approximations.
The values of all complex components 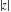 , , 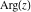 , , 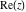 , , 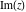 , ,  , and , and  at the points at the points 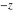 , ,  , –ⅈ z, , –ⅈ z, 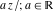 , , 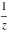 , ,  , , 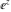 , and , and 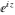 are given by the following identities: are given by the following identities:
The values of all complex components 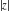 , , 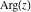 , , 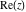 , , 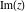 , , 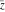 , and , and 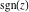 at the points at the points 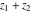 , , 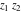 , and , and 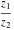 are described by the following table: are described by the following table:
Some complex components can be easily evaluated in more general cases of the points including symbolic sums and products of  , ,  , for example: , for example:
The previous tables and formulas can be modified or simplified for particular cases when some variables become real or satisfy special restrictions, for example:
Taking into account that complex components have numerous representations through other complex components and elementary functions such as the logarithm, exponential function, or the inverse tangent function, all of the previous formulas can be transformed into different equivalent forms. Here are some of the resulting formulas for the power function 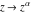 : :
Similar identities can be derived for the exponent functions, such as:
Some arithmetical operations involving complex components or elementary functions of complex components are:
The next two tables describe all the complex components applied to all complex components 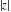 , , 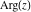 , ,  , , 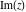 , , 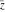 , and , and 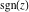 at the points at the points 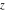 and and  : :
The derivatives of five complex components 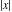 , , 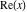 , , 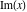 , , 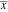 , and , and 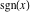 at the real point at the real point 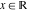 can be interpreted in a real‐analytic or distributional sense and are given by the following formulas: can be interpreted in a real‐analytic or distributional sense and are given by the following formulas:
where  is the Dirac delta function. is the Dirac delta function.
It is impossible to make a classical, direction-independent interpretation of these derivatives for complex values of variable  because the complex components do not fulfill the Cauchy-Riemann conditions. because the complex components do not fulfill the Cauchy-Riemann conditions.
The indefinite integrals of some complex components at the real point 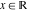 can be represented by the following formulas: can be represented by the following formulas:
The definite integrals of some complex components in the complex plane can also be represented through complex components, for example:
Some definite integrals including absolute values can be easily evaluated, for example (in the Hadamard sense of integration, the next identity is correct for all complex values of 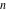 ): ):
Fourier integral transforms of the absolute value and signum functions 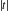 and and 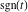 can be evaluated through generalized functions: can be evaluated through generalized functions:
Laplace integral transforms of these functions can be evaluated in a classical sense and have the following values:
The absolute value function 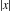 for real for real 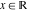 satisfies the following simple first-order differential equation understandable in a distributional sense: satisfies the following simple first-order differential equation understandable in a distributional sense:
In a similar manner:
All six complex components 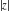 , , 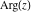 , , 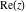 , , 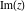 , ,  and and 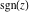 satisfy numerous inequalities. The best known are so-called triangle inequalities for absolute values: satisfy numerous inequalities. The best known are so-called triangle inequalities for absolute values:
Some other inequalities can be described by the following formulas:
The six complex components 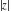 , , 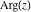 , , 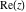 , , 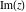 , ,  , and , and  have the set of zeros described by the following formulas: have the set of zeros described by the following formulas:
|