|
The concepts of indeterminate, infinity, and directed infinity surfaced in mathematics on an intuitive level many centuries ago. For example, it was clear that it was not possible to find the largest integer. Euclid already proved that the largest prime number (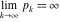 in modern notations) does not exist. in modern notations) does not exist.
The modern mathematical symbol arose with the development of calculus. J. Wallis (1655) introduced the sign ∞ to signify infinite numbers. Subsequently many mathematicians started to use this or similar symbols. In the twentieth century, K. Weierstrass (1876) used the symbol ∞ to represent an actual infinite quantity.
The mathematical symbols used to designate an indeterminant quantity also came from calculus. L'Hospital (1696) treated the sign 0/0 as an indeterminate value. Later, J. Bernoulli (1704, 1730), G. Cramer (1732), J. D'Alembert (1754), and others extensively discussed the symbol 0/0 and tried to introduce special notation for it. The appearance of the modern definition of a limit allowed for an evolving understanding of indeterminate quantities, like 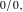 to have all possible values of the double limit of to have all possible values of the double limit of 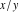 , when variables , when variables 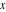 and and 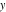 tend to be tend to be 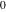 independently (at different rates). independently (at different rates).
|