|
Introduction to the symbols
General
The concepts of indeterminate, infinity, and directed infinity surfaced in mathematics on an intuitive level many centuries ago. For example, it was clear that it was not possible to find the largest integer. Euclid already proved that the largest prime number (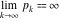 in modern notations) does not exist. in modern notations) does not exist.
The modern mathematical symbol arose with the development of calculus. J. Wallis (1655) introduced the sign ∞ to signify infinite numbers. Subsequently many mathematicians started to use this or similar symbols. In the twentieth century, K. Weierstrass (1876) used the symbol ∞ to represent an actual infinite quantity.
The mathematical symbols used to designate an indeterminant quantity also came from calculus. L'Hospital (1696) treated the sign 0/0 as an indeterminate value. Later, J. Bernoulli (1704, 1730), G. Cramer (1732), J. D'Alembert (1754), and others extensively discussed the symbol 0/0 and tried to introduce special notation for it. The appearance of the modern definition of a limit allowed for an evolving understanding of indeterminate quantities, like 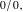 to have all possible values of the double limit of to have all possible values of the double limit of 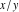 , when variables , when variables 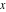 and and 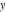 tend to be tend to be 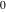 independently (at different rates). independently (at different rates).
Definitions of symbols
There are four symbols discussed here—an indeterminate numerical quantity 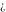 , infinity , infinity 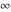 , complex infinity , complex infinity 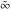 , and directed infinity in the complex plane , and directed infinity in the complex plane  . They are defined as follows: . They are defined as follows:
Indeterminate 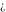 is a symbol that represents a numerical quantity whose magnitude cannot be determined. In particular, arbitrary functions with any argument being is a symbol that represents a numerical quantity whose magnitude cannot be determined. In particular, arbitrary functions with any argument being 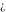 also becomes also becomes 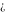 : :  . .
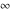 is a symbol that represents a positive infinite quantity. is a symbol that represents a positive infinite quantity.
∞~ represents an infinite numerical quantity whose direction in the complex plane is unknown (undetermined).
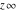 represents an infinite numerical quantity that is a positive real multiple of the complex number represents an infinite numerical quantity that is a positive real multiple of the complex number 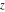 . .
Connections within the group of symbols and with other function groups
Representations through related functions
The symbols 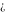 , , 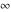 , and , and  are connected to each other by the following formulas, including the operations plus, subtract, times, divide, and power: are connected to each other by the following formulas, including the operations plus, subtract, times, divide, and power:
Representations through other functions
Some of the symbols 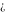 , , 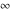 , , 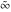 , and , and 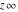 can be represented as values of basic arithmetic operations, for example: can be represented as values of basic arithmetic operations, for example:
Some of the symbols 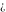 , , 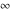 , , 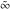 , and , and 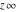 can be represented as values of different mathematical functions, for example: can be represented as values of different mathematical functions, for example:
The best-known properties and formulas for symbols
Specific values
The symbol  has the following values at some finite points has the following values at some finite points 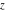 : :
The symbol 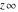 has the following values at some infinite points has the following values at some infinite points  : :
The symbol  has the following value at point has the following value at point 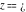 : :
General characteristics
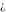 is a symbol. It represents an unknown or not exactly determined point (potentially with infinite magnitude) of the complex plane. Often it results from a double limit where two infinitesimal parameters approach zero at different speeds (e.g. is a symbol. It represents an unknown or not exactly determined point (potentially with infinite magnitude) of the complex plane. Often it results from a double limit where two infinitesimal parameters approach zero at different speeds (e.g. 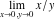 ). ).
 is a symbol. On the Riemann sphere, it is the north pole approached from exactly east. In the projective complex plane, it is a point at the line at infinity. is a symbol. On the Riemann sphere, it is the north pole approached from exactly east. In the projective complex plane, it is a point at the line at infinity.
 is a symbol. On the Riemann sphere, it is the north pole. In the projective complex plane, it is the line at infinity. is a symbol. On the Riemann sphere, it is the north pole. In the projective complex plane, it is the line at infinity.
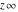 is a symbol. On the Riemann sphere, it is the north pole together with the direction is a symbol. On the Riemann sphere, it is the north pole together with the direction 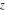 how to approach it. In the projective complex plane, it is a point at the line at infinity. how to approach it. In the projective complex plane, it is a point at the line at infinity.
Complex characteristics
The symbols 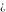 , , 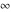 , , 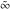 , and , and 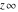 have the following complex characteristics: have the following complex characteristics:
Differentiation
Derivatives of the symbols 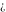 , ,  , , 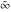 , and , and 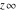 satisfy the following relations: satisfy the following relations:
Integration
Simple indefinite integrals of the symbols 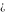 , ,  , and , and 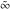 have the following representations: have the following representations:
Integral transforms
All Fourier integral transforms of the symbols 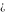 , , 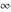 , , 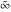 , and , and 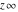 can be evaluated using the following formal rules: can be evaluated using the following formal rules:
Laplace direct and inverse integral transforms of the symbols 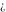 , , 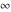 , , 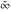 , and , and 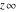 can be evaluated using the following formal rules: can be evaluated using the following formal rules:
Inequalities
The symbols  , , 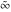 , and , and 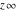 satisfy some obvious inequalities, for example: satisfy some obvious inequalities, for example:
Applications of the symbols
All symbols are used throughout mathematics, the exact sciences, and engineering.
|