|
The imaginary unit 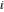 satisfies the following relation: satisfies the following relation:
For evaluation of the eight classical constants 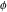 , , 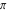 , ,  , , 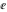 , , 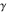 , , 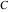 , , 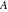 , and , and 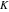 , Mathematica uses procedures that are based on the following formulas or methods: , Mathematica uses procedures that are based on the following formulas or methods:
The formula for 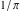 is called Chudnovsky's formula. is called Chudnovsky's formula.
The eight classical constants 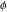 , , 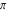 , ,  , , 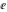 , , 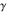 , , 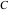 , , 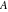 , and , and 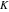 are positive real numbers. The constant are positive real numbers. The constant 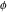 is a quadratic irrational number. The constants is a quadratic irrational number. The constants 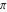 , , 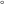 , and , and 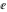 are irrational and transcendental over are irrational and transcendental over 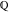 . Whether . Whether 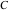 and and 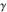 are irrational is not known.
The imaginary unit are irrational is not known.
The imaginary unit 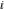 is an algebraic number. is an algebraic number.
The five classical constants 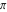 , , 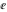 , , 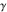 , , 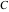 , and , and 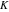 have numerous series representations, for example, the following: have numerous series representations, for example, the following:
The four classical constants 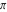 , , 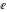 , , 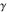 , and , and 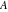 can be represented by the following formulas: can be represented by the following formulas:
The five classical constants 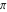 , (and , (and 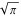 ), ), 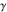 , , 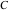 , , 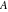 , and , and 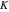 have numerous integral representations, for example: have numerous integral representations, for example:
The following integral is called the Gaussian probability density integral:
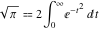 . .
The following integrals are called the Fresnel integrals:
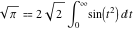
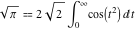 . .
The six classical constants 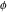 , , 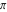 , , 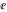 , , 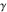 , , 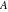 , and , and 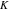 have numerous limit representations, for example: have numerous limit representations, for example:
The four classical constants 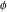 , , 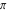 , , 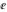 , and , and 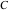 have numerous closed‐form continued fraction representations, for example: have numerous closed‐form continued fraction representations, for example:
The golden ratio 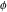 satisfies the following special functional identities: satisfies the following special functional identities:
The eight classical constants (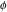 , , 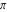 , , 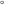 , , 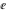 , , 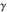 , , 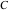 , , 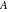 , and , and 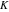 ) and the imaginary unit ) and the imaginary unit 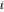 have the following complex characteristics: have the following complex characteristics:
Derivatives of the eight classical constants (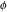 , , 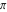 , , 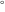 , , 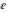 , , 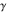 , , 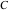 , , 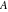 , and , and 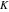 ) and imaginary unit constant ) and imaginary unit constant 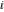 satisfy the following relations: satisfy the following relations:
Simple indefinite integrals of the eight classical constants (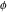 , , 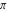 , , 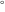 , , 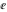 , , 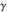 , , 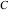 , , 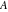 , and , and 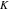 ) and imaginary unit constant ) and imaginary unit constant 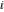 have the following values: have the following values:
All Fourier integral transforms and Laplace direct and inverse integral transforms of the eight classical constants (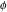 , , 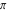 , , 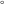 , , 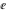 , , 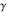 , , 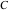 , , 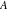 , and , and 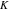 ) and the imaginary unit ) and the imaginary unit 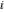 can be evaluated in a distributional or classical sense and can include the Dirac delta function: can be evaluated in a distributional or classical sense and can include the Dirac delta function:
The eight classical constants (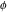 , , 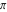 , , 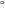 , , 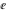 , , 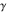 , , 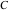 , , 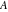 , and , and 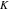 ) satisfy numerous inequalities, for example: ) satisfy numerous inequalities, for example:
|