|
The best-known properties and formulas for symbols
Specific values
The symbol 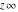 has the following values at some finite points has the following values at some finite points 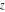 : :
The symbol 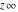 has the following values at some infinite points has the following values at some infinite points 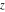 : :
The symbol 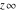 has the following value at point has the following value at point 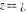 : :
General characteristics
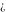 is a symbol. It represents an unknown or not exactly determined point (potentially with infinite magnitude) of the complex plane. Often it results from a double limit where two infinitesimal parameters approach zero at different speeds (e.g. is a symbol. It represents an unknown or not exactly determined point (potentially with infinite magnitude) of the complex plane. Often it results from a double limit where two infinitesimal parameters approach zero at different speeds (e.g. 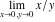 ). ).
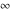 is a symbol. On the Riemann sphere, it is the north pole approached from exactly east. In the projective complex plane, it is a point at the line at infinity. is a symbol. On the Riemann sphere, it is the north pole approached from exactly east. In the projective complex plane, it is a point at the line at infinity.
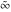 is a symbol. On the Riemann sphere, it is the north pole. In the projective complex plane, it is the line at infinity. is a symbol. On the Riemann sphere, it is the north pole. In the projective complex plane, it is the line at infinity.
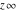 is a symbol. On the Riemann sphere, it is the north pole together with the direction is a symbol. On the Riemann sphere, it is the north pole together with the direction 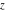 how to approach it. In the projective complex plane, it is a point at the line at infinity. how to approach it. In the projective complex plane, it is a point at the line at infinity.
Complex characteristics
The symbols 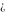 , , 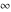 , , 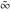 , and , and 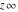 have the following complex characteristics: have the following complex characteristics:
Differentiation
Derivatives of the symbols 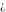 , , 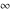 , , 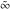 , and , and 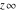 satisfy the following relations: satisfy the following relations:
Integration
Simple indefinite integrals of the symbols 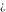 , , 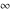 , and , and 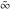 have the following representations: have the following representations:
Integral transforms
All Fourier integral transforms of the symbols 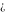 , , 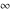 , , 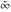 , and , and 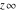 can be evaluated using the following formal rules: can be evaluated using the following formal rules:
Laplace direct and inverse integral transforms of the symbols 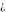 , , 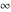 , , 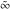 , and , and 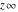 can be evaluated using the following formal rules: can be evaluated using the following formal rules:
Inequalities
The symbols 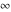 , , 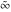 , and , and 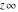 satisfy some obvious inequalities, for example: satisfy some obvious inequalities, for example:
|