|
Plots of random walks based on the digits 1D walks 1D random walks based on the digits  of of 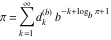 in various bases. If in various bases. If 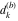 is even, a step to the right is taken, if is even, a step to the right is taken, if 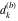 is odd, a step to the left is taken. is odd, a step to the left is taken. 1D random walks based on the digits 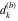 of of 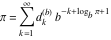 in various bases. If in various bases. If 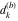 is even, a step to the right is taken, if is even, a step to the right is taken, if 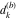 is odd, a step to the left is taken. The left graphic shows the average distance of the walker from the origin, averaged over the first 100 even bases is odd, a step to the left is taken. The left graphic shows the average distance of the walker from the origin, averaged over the first 100 even bases 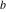 . The right graphic shows the binned scaled deviation of the individual walks (for a fixed basis . The right graphic shows the binned scaled deviation of the individual walks (for a fixed basis 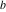 ) from the average. ) from the average. 2D walks 2D random walks based on the digits 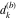 of of 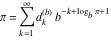 in various bases in various bases 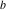 . For each . For each 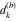 , a step is taken in direction , a step is taken in direction 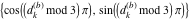 . For clarity, the . For clarity, the 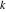 th step is shown with a th step is shown with a 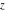 ‐value ‐value 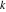 . . 2D random walks based on the digits 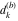 of of 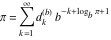 in various bases in various bases 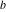 . For each . For each 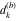 , a step is taken in direction , a step is taken in direction  . For clarity, the . For clarity, the 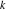 th step is shown with a th step is shown with a 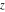 ‐value ‐value 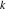 . . 2D random walks based on the digits 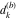 of of  in various bases in various bases 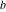 . For each . For each  , a step is taken in direction , a step is taken in direction 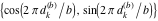 . . 2D random walks based on the digits 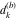 of of 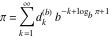 in various bases in various bases 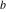 . For each . For each  a step is taken in direction a step is taken in direction  . . Platonic walks 3D random walks based on the digits  of of 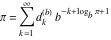 in various bases in various bases  . For each . For each 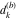 , a step of size 1 is taken in direction of the , a step of size 1 is taken in direction of the 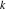 th vertex of a Platonic solid. th vertex of a Platonic solid. 2D Levy-type walks 2D Lévy‐type random walks based on the digits 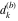 of of 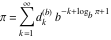 in various bases in various bases 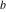 and numbers of directions and numbers of directions  . For each . For each 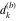 , a step of length , a step of length 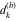 is taken in direction is taken in direction 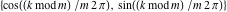 . . Higher-dimensional walks 2D projections of a  D random walk based on the digits D random walk based on the digits 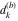 of of 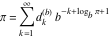 in various bases in various bases 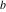 . For each . For each 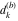 , a step is taken in direction , a step is taken in direction  (the (the 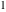 is on position is on position 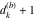 ). The resulting visited lattice points are projected into a 2D plane spanned by the vectors ). The resulting visited lattice points are projected into a 2D plane spanned by the vectors  and and 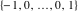 . .
|