|
Continued fraction digits Plots of the simple continued fraction digits 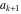 of of 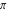 . . Plots of  of the simple continued fraction digits of the simple continued fraction digits 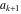 of of 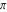 . For almost all numbers, this sequence converges to the Khinchin constant . For almost all numbers, this sequence converges to the Khinchin constant 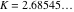 . . Plots of 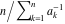 of the simple continued fraction digits of the simple continued fraction digits 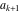 of of 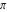 in various bases. For almost all numbers, this sequence converges to the Khinchin harmonic mean in various bases. For almost all numbers, this sequence converges to the Khinchin harmonic mean 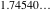 . . Plots of 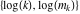 where where 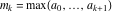 and and 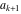 are the simple continued fraction digits of are the simple continued fraction digits of 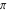 . . Ratio between the actual number of occurrences of the digit 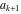 in the simple continued fraction expansion of in the simple continued fraction expansion of 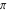 to the expected number according to the Gauss–Kuzmin distribution law. to the expected number according to the Gauss–Kuzmin distribution law. Continued fraction convergents Difference of the scaled convergents 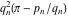 of the simple continued fraction expansion of of the simple continued fraction expansion of 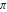 . . The 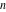 th root of the denominator th root of the denominator 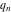 of the convergents of the convergents 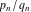 of the simple continued fraction expansion of of the simple continued fraction expansion of 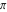 . For almost all numbers, this sequence converges to the Khinchin–Levy constant . For almost all numbers, this sequence converges to the Khinchin–Levy constant 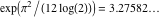 . . The number of correct decimal digits minus 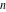 of the of the 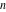 th convergents of the simple continued fraction expansion of th convergents of the simple continued fraction expansion of 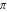 . By Lochs' theorem for almost all numbers, the . By Lochs' theorem for almost all numbers, the 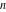 th convergent gives th convergent gives 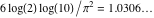 correct decimal digits. correct decimal digits. Nested differences, sums, products, and quotients Iterated pairwise sums (left) and differences (right) modulo 2 starting with the first 200 simple continued fraction digits 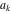 of of 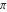 . . Cellular automata plots Evolution of the elementary cellular automata with initial conditions 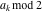 where the where the 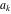 ere the simple continued fraction digits ere the simple continued fraction digits 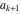 of of 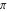 . . Continued fraction values of base b digits Values obtained by interpreting the base 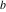 digits digits 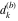 of of 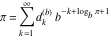 as the simple continued fraction digits of a number. as the simple continued fraction digits of a number. Values obtained by interpreting the base 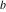 digits digits 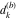 of of 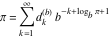 as the continued fraction digits of a number. as the continued fraction digits of a number. Values obtained by interpreting the base 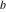 digits digits 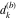 of of 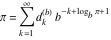 as the continued fraction digits of a number for noninteger bases. as the continued fraction digits of a number for noninteger bases. Eigenvalue plots Eigenvalues in the complex plane of the square matrices formed from the first 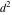 digits of the simple continued fraction expansion digits of the simple continued fraction expansion 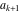 of of 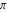 , ,  . The eigenvalues are colored from red ( . The eigenvalues are colored from red (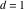 ) to blue ( ) to blue (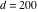 ). ). Eigenvalues in the complex plane of the square matrices formed from the first digits 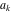 of the simple continued fraction expansion of of the simple continued fraction expansion of 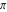 . The matrix formed is . The matrix formed is 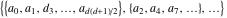 . The eigenvalues are colored from red ( . The eigenvalues are colored from red (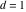 ) to blue ( ) to blue (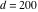 ). ). Root plots Zeros of the polynomials 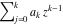 of the digits of the simple continued fraction expansion of the digits of the simple continued fraction expansion 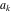 of of 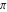 over the complex plane. over the complex plane. Fourier series Fejer averages of the exponential Fourier series 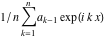 , , 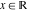 over the complex plane. Here the over the complex plane. Here the 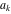 are the digits of the simple continued fraction of are the digits of the simple continued fraction of 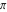 . The coloring of the curves varies from red ( . The coloring of the curves varies from red (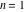 ) to violet ( ) to violet (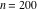 ). ). Pascal triangle modular plots Density plot of the digits 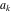 of the simple continued fraction of of the simple continued fraction of 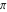 . The first . The first 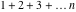 digits are extracted and arranged in a triangle and colored according to their value modulo digits are extracted and arranged in a triangle and colored according to their value modulo 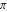 , two and three. , two and three. Power series plots 3D plots of the power series 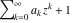 . Here, . Here, 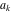 is the is the 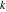 th digit of the simple continued fraction of th digit of the simple continued fraction of 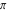 . The left graphic shows the real part and the coloring is according to the imaginary part. The right graphic shows a contour plot of the argument over the complex plane and the coloring is cyclic. . The left graphic shows the real part and the coloring is according to the imaginary part. The right graphic shows a contour plot of the argument over the complex plane and the coloring is cyclic. Density plots of coefficients of 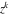 of the power series of the power series 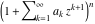 . Here, . Here, 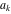 is the is the 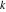 th digit of the simple continued fraction of th digit of the simple continued fraction of 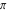 . The left graphic shows the coefficients modulo 2 and the right graphic shows the coefficients modulo . The left graphic shows the coefficients modulo 2 and the right graphic shows the coefficients modulo 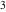 . .
|