|
Approximation properties Scaled minimal distance of the nearest rational number 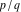 with a given denominator with a given denominator 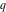 to to 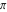 . The graphic shows . The graphic shows 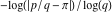 . . Convergence of some sum and limit representations Convergents of the representation 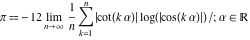 for for 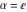 as a function of as a function of 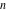 . . Convergence of the representation 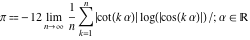 as a function of as a function of 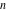 and and 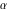 . . Convergence of the representation 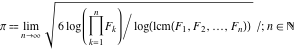 as a function of as a function of 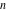 . Here the . Here the 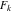 are the Fibonacci numbers. are the Fibonacci numbers. Parametrized curves 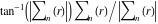 for for 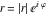 for various for various 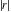 over the complex plane. Here over the complex plane. Here 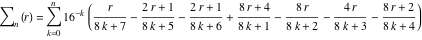 is the truncated sum of the generalized Bailey–Borwein–Plouffe algorithm. The black dot indicates the value of is the truncated sum of the generalized Bailey–Borwein–Plouffe algorithm. The black dot indicates the value of 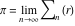 . . Fractional parts of the Beatty sequences Fractional parts of the numbers of the Beatty sequences 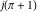 , , 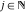 , , 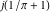 , , 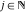 that lie in the intervals that lie in the intervals 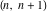 . . Nested binary operations Values over the complex plane of the nested binary operations addition, subtraction, multiplication, and division using the arguments 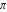 , , 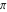 , , 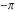 , , 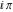 , , 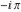 , and , and 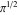 . . Pseudorandom structures Random binary trees based on the digits of 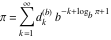 in various bases in various bases 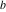 . Starting with the root, recursively new branches are formed if . Starting with the root, recursively new branches are formed if 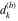 is odd. The is odd. The 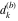 are used in their natural order, starting with are used in their natural order, starting with 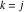 . . Points generated by iteratively reflecting a point on the 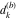 th edge of an th edge of an 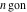 . The first point is the origin and the . The first point is the origin and the 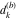 are the digits of are the digits of 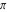 in various base in various base 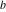 . . Iterations of the map 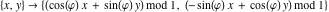 starting with homogeneously distributed points of the unit square. The points are colored from red to blue with increasing iteration number. starting with homogeneously distributed points of the unit square. The points are colored from red to blue with increasing iteration number. Iterations of the map 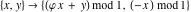 starting with homogeneously distributed points of the unit square. The points are colored from red to blue with increasing iteration number. starting with homogeneously distributed points of the unit square. The points are colored from red to blue with increasing iteration number.
|