|
2D plots along the axes and unit circle On the real axis The function 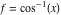 along the real axis. along the real axis. 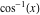 is real‐valued for arguments from the interval is real‐valued for arguments from the interval  . . The function 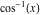 along the real axis. Outside the interval along the real axis. Outside the interval 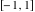 , the function , the function  has a constant real part ( has a constant real part (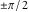 ) and a nonvanishing imaginary part. The left graphic shows ) and a nonvanishing imaginary part. The left graphic shows  and the right graphic shows and the right graphic shows 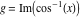 . . The absolute value and the argument of  along the real axis. The left graphic shows along the real axis. The left graphic shows  and the right graphic shows and the right graphic shows 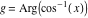 . For . For 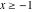 , the argument is piecewise constant. , the argument is piecewise constant. On the real axis at infinity The function 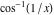 along the real axis. The left graphic shows along the real axis. The left graphic shows 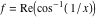 and the right graphic shows and the right graphic shows 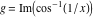 . At . At  , the function , the function 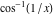 has a logarithmic singularity. has a logarithmic singularity. The absolute value and the argument of 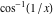 along the real axis. The left graphic shows along the real axis. The left graphic shows 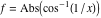 and the right graphic shows and the right graphic shows  . For . For  , the argument is piecewise constant. , the argument is piecewise constant. On the imaginary axes The real part and the imaginary part of 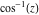 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 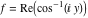 , and the right graphic shows , and the right graphic shows 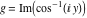 . Along the imaginary axis, . Along the imaginary axis,  is complex valued with a constant imaginary part and it is logarithmically increasing. is complex valued with a constant imaginary part and it is logarithmically increasing. The absolute value and the argument of 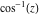 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 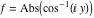 and the right graphic shows and the right graphic shows 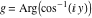 . Because . Because 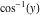 is purely imaginary on the imaginary axis, the argument is piecewise constant. is purely imaginary on the imaginary axis, the argument is piecewise constant. On the imaginary axis at infinity The function 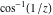 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 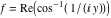 and the right graphic shows and the right graphic shows 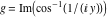 . At . At  , the function , the function 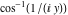 has a logarithmic singularity. has a logarithmic singularity. The absolute value and the argument of 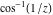 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 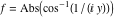 and the right graphic shows and the right graphic shows 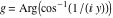 . . On the unit circle The real part and the imaginary part of 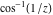 on the unit circle. The left graphic shows on the unit circle. The left graphic shows  and the right graphic shows and the right graphic shows 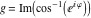 . . The absolute value and the argument of 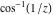 on the unit circle. The left graphic shows on the unit circle. The left graphic shows 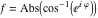 and the right graphic shows and the right graphic shows 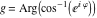 . .
|