|
2D plots along the axes and unit circle On the real axis The function 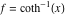 along the real axis. along the real axis. 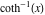 is real‐valued in the interval is real‐valued in the interval 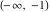 and and 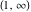 . At . At 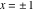 , the function , the function 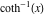 has logarithmic singularities. has logarithmic singularities. The function 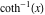 along the real axis. The left graphic shows along the real axis. The left graphic shows 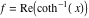 and the right graphic shows and the right graphic shows 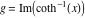 . In the interval . In the interval 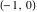 the function the function 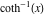 is purely imaginary and the real part vanishes identically. is purely imaginary and the real part vanishes identically. The absolute value and the argument of 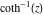 along the real axis. The left graphic shows along the real axis. The left graphic shows 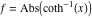 and the right graphic shows and the right graphic shows 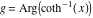 . . On the real axis at infinity The function 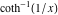 along the real axis. The left graphic shows along the real axis. The left graphic shows 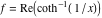 and the right graphic shows and the right graphic shows 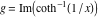 . . The absolute value and the argument of 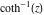 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 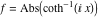 and the right graphic shows and the right graphic shows 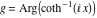 . . On the imaginary axes The real part and the imaginary part of 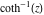 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 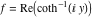 and the right graphic shows and the right graphic shows 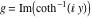 . Along the imaginary axis, the real part of . Along the imaginary axis, the real part of 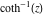 vanishes identically. vanishes identically. The absolute value and the argument of 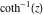 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 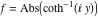 and the right graphic shows and the right graphic shows 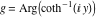 . . On the imaginary axis at infinity The function 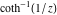 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 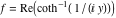 and the right graphic shows and the right graphic shows 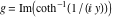 . . The absolute value and the argument of 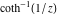 along the imaginary axis. The left graphic shows along the imaginary axis. The left graphic shows 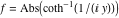 and the right graphic shows and the right graphic shows 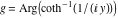 . . On the unit circle The real part and the imaginary part of 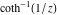 on the unit circle. The left graphic shows on the unit circle. The left graphic shows 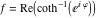 and the right graphic shows and the right graphic shows 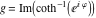 . . The absolute value and the argument of 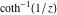 on the unit circle. The left graphic shows on the unit circle. The left graphic shows 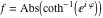 and the right graphic shows and the right graphic shows 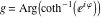 . .
|