|
Introduction to the trigonometric functions
General
The six trigonometric functions sine 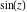 , cosine , cosine 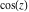 , tangent , tangent 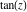 , cotangent , cotangent 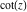 , cosecant , cosecant  , and secant , and secant  are well known and among the most frequently used elementary functions. The most popular functions are well known and among the most frequently used elementary functions. The most popular functions 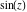 , ,  , , 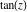 , and , and 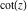 are taught worldwide in high school programs because of their natural appearance in problems involving angle measurement and their wide applications in the quantitative sciences. are taught worldwide in high school programs because of their natural appearance in problems involving angle measurement and their wide applications in the quantitative sciences.
The trigonometric functions share many common properties.
Definitions of trigonometric functions
All trigonometric functions can be defined as simple rational functions of the exponential function of 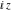 : :
The functions 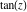 , , 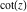 , , 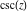 , and , and 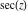 can also be defined through the functions can also be defined through the functions 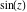 and and 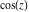 using the following formulas: using the following formulas:
A quick look at the trigonometric functions Here is a quick look at the graphics for the six trigonometric functions along the real axis.
Connections within the group of trigonometric functions and with other function groups
Representations through more general functions
The trigonometric functions are particular cases of more general functions. Among these more general functions, four different classes of special functions are particularly relevant: Bessel, Jacobi, Mathieu, and hypergeometric functions.
For example, 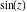 and and 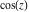 have the following representations through Bessel, Mathieu, and hypergeometric functions: have the following representations through Bessel, Mathieu, and hypergeometric functions:
On the other hand, all trigonometric functions can be represented as degenerate cases of the corresponding doubly periodic Jacobi elliptic functions when their second parameter is equal to 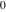 or or 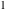 : :
Representations through related equivalent functions
Each of the six trigonometric functions can be represented through the corresponding hyperbolic function:
Relations to inverse functions
Each of the six trigonometric functions is connected with its corresponding inverse trigonometric function by two formulas. One is a simple formula, and the other is much more complicated because of the multivalued nature of the inverse function:
Representations through other trigonometric functions
Each of the six trigonometric functions can be represented by any other trigonometric function as a rational function of that function with linear arguments. For example, the sine function can be representative as a group‐defining function because the other five functions can be expressed as follows:
All six trigonometric functions can be transformed into any other trigonometric function of this group if the argument 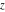 is replaced by is replaced by 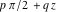 with with 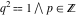 : :
The best-known properties and formulas for trigonometric functions
Real values for real arguments
For real values of argument 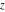 , the values of all the trigonometric functions are real (or infinity). , the values of all the trigonometric functions are real (or infinity).
In the points 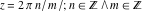 , the values of trigonometric functions are algebraic. In several cases they can even be rational numbers or integers (like , the values of trigonometric functions are algebraic. In several cases they can even be rational numbers or integers (like 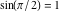 or or 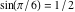 ). The values of trigonometric functions can be expressed using only square roots if ). The values of trigonometric functions can be expressed using only square roots if  and and  is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}. is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}.
Simple values at zero
All trigonometric functions have rather simple values for arguments  and and 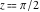 : :
Analyticity
All trigonometric functions are defined for all complex values of 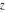 , and they are analytical functions of , and they are analytical functions of 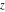 over the whole complex over the whole complex 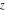 ‐plane and do not have branch cuts or branch points. The two functions ‐plane and do not have branch cuts or branch points. The two functions  and and  are entire functions with an essential singular point at are entire functions with an essential singular point at  . All other trigonometric functions are meromorphic functions with simple poles at points . All other trigonometric functions are meromorphic functions with simple poles at points 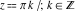 for for 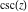 and and  , and at points , and at points 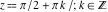 for for 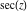 and and 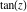 . .
Periodicity
All trigonometric functions are periodic functions with a real period (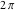 or or 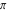 ): ):
Parity and symmetry
All trigonometric functions have parity (either odd or even) and mirror symmetry:
Simple representations of derivatives
The derivatives of all trigonometric functions have simple representations that can be expressed through other trigonometric functions:
Simple differential equations
The solutions of the simplest second‐order linear ordinary differential equation with constant coefficients can be represented through 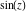 and and  : :
All six trigonometric functions satisfy first-order nonlinear differential equations:
Applications of trigonometric functions
Triangle theorems
The prime application of the trigonometric functions are triangle theorems. In a triangle, 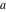 , ,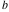 , and , and 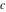 represent the lengths of the sides opposite to the angles, Δ the area , represent the lengths of the sides opposite to the angles, Δ the area , 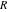 the circumradius, and the circumradius, and 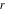 the inradius. Then the following identities hold: the inradius. Then the following identities hold:
For a right‐angle triangle the following relations hold:
Other applications
Because the trigonometric functions appear virtually everywhere in quantitative sciences, it is impossible to list their numerous applications in teaching, science, engineering, and art.
|