|
The function 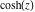 is a particular case of more complicated mathematical functions. For example, it is a special case of the generalized hypergeometric function is a particular case of more complicated mathematical functions. For example, it is a special case of the generalized hypergeometric function  with the parameter with the parameter 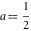 at at 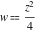 : :
It is also a particular case of the modified Bessel function 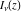 with the parameter with the parameter 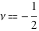 , multiplied by , multiplied by 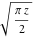 : :
Other Bessel functions can also be expressed through hyperbolic cosine functions for similar values of the parameter:
Struve functions can also degenerate into the hyperbolic cosine function for a similar value of the parameter:
But the function 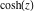 is also a degenerate case of the doubly periodic Jacobi elliptic functions when their second parameter is equal to is also a degenerate case of the doubly periodic Jacobi elliptic functions when their second parameter is equal to 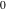 or or 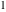 : :
Finally, the function 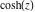 is the particular case of one more class of functions—the Mathieu functions: is the particular case of one more class of functions—the Mathieu functions:
|