|
Almost everybody prefers using 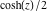 instead of instead of 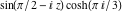 . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can give overly complicated results. Compact expressions like . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can give overly complicated results. Compact expressions like 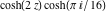 should not be automatically expanded into the more complicated expression should not be automatically expanded into the more complicated expression 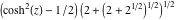 . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section. . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section.
The function TrigExpand expands out trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in the arguments of trigonometric and hyperbolic functions, and then expands out the products of trigonometric and hyperbolic functions into sums of powers, using trigonometric and hyperbolic identities where possible. Here are some examples.
The function TrigFactor factors trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in arguments of trigonometric and hyperbolic functions, and then factors the resulting polynomials into trigonometric and hyperbolic functions, using trigonometric and hyperbolic identities where possible. Here are some examples.
The function TrigReduce rewrites the products and powers of trigonometric and hyperbolic functions in terms of trigonometric and hyperbolic functions with combined arguments. In more detail, it typically yields a linear expression that involves trigonometric and hyperbolic functions with more complicated arguments. TrigReduce is approximately inverse to TrigExpand and TrigFactor. Here are some examples.
The function TrigToExp converts trigonometric and hyperbolic functions to exponentials. It tries, where possible, to give results that do not involve explicit complex numbers. Here are some examples.
The function ExpToTrig converts exponentials to trigonometric and hyperbolic functions. It is approximately inverse to TrigToExp. Here are some examples.
The function ComplexExpand expands expressions assuming that all the variables are real. The value option TargetFunctions is a list of functions from the set {Re, Im, Abs, Arg, Conjugate, Sign}. ComplexExpand tries to give results in terms of the functions specified. Here are some examples.
The function Simplify performs a sequence of algebraic transformations on its argument, and returns the simplest form it finds. Here are some examples.
Here is a large collection of hyperbolic identities. Each is written as a logical conjunction.
The function Simplify has the Assumption option. For example, Mathematica knows that 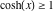 for all real for all real 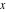 , and recognizes the periodicity of hyperbolic functions for the symbolic integer coefficient , and recognizes the periodicity of hyperbolic functions for the symbolic integer coefficient 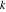 of of 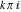 . .
Mathematica also knows that the composition of the inverse and direct hyperbolic functions gives the value of the internal argument under the corresponding restriction.
While the hyperbolic cosine function auto‐evaluates for simple fractions of  , for more complicated cases it stays as a hyperbolic cosine function to avoid the build up of large expressions. Using the function FunctionExpand, the hyperbolic cosine function can sometimes be transformed into explicit radicals. Here are some examples. , for more complicated cases it stays as a hyperbolic cosine function to avoid the build up of large expressions. Using the function FunctionExpand, the hyperbolic cosine function can sometimes be transformed into explicit radicals. Here are some examples.
If the denominator contains squares of integers other than 2, the results always contain complex numbers (meaning that the imaginary number 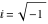 appears unavoidably). appears unavoidably).
The function RootReduce allows for writing the last algebraic numbers as roots of polynomial equations.
The function FunctionExpand also reduces hyperbolic expressions with compound arguments or compositions, including inverse hyperbolic functions, to simpler ones. Here are some examples.
Applying Simplify to the last expression gives a more compact result.
The function FullSimplify tries a wider range of transformations than Simplify and returns the simplest form it finds. Here are some examples that compare the results of applying the functions Simplify and FullSimplify to the same expressions.
|