|
The cotangent function is an old mathematical function. It was mentioned in 1620 by E. Gunter who invented the notation of "cotangens". Later on J. Keill (1726) and L. Euler (1748) used this function and its notation 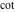 in their investigations. in their investigations.
The classical definition of the cotangent function for real arguments is: "the cotangent of an angle 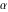 in a right‐angle triangle is the ratio of the length of the adjacent leg to the length to the opposite leg." This description of in a right‐angle triangle is the ratio of the length of the adjacent leg to the length to the opposite leg." This description of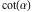 is valid for is valid for 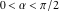 when the triangle is nondegenerate. This approach to the cotangent can be expanded to arbitrary real values of when the triangle is nondegenerate. This approach to the cotangent can be expanded to arbitrary real values of 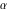 if consideration is given to the arbitrary point if consideration is given to the arbitrary point  in the in the 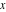 , ,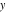 ‐Cartesian plane and ‐Cartesian plane and 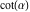 is defined as the ratio is defined as the ratio 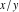 assuming that α is the value of the angle between the positive direction of the assuming that α is the value of the angle between the positive direction of the 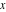 ‐axis and the direction from the origin to the point ‐axis and the direction from the origin to the point 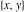 . .
Comparing the cotangent definition with the definitions of the sine and cosine functions shows that the following formula can also be used as a definition of the cotangent function:
|