|
Introduction to the Cotangent Function
Defining the cotangent function
The cotangent function is an old mathematical function. It was mentioned in 1620 by E. Gunter who invented the notation of "cotangens". Later on J. Keill (1726) and L. Euler (1748) used this function and its notation 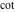 in their investigations. in their investigations.
The classical definition of the cotangent function for real arguments is: "the cotangent of an angle 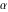 in a right‐angle triangle is the ratio of the length of the adjacent leg to the length to the opposite leg." This description of in a right‐angle triangle is the ratio of the length of the adjacent leg to the length to the opposite leg." This description of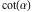 is valid for is valid for 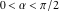 when the triangle is nondegenerate. This approach to the cotangent can be expanded to arbitrary real values of when the triangle is nondegenerate. This approach to the cotangent can be expanded to arbitrary real values of 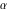 if consideration is given to the arbitrary point if consideration is given to the arbitrary point  in the in the 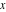 , ,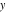 ‐Cartesian plane and ‐Cartesian plane and 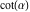 is defined as the ratio is defined as the ratio 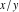 assuming that α is the value of the angle between the positive direction of the assuming that α is the value of the angle between the positive direction of the 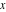 ‐axis and the direction from the origin to the point ‐axis and the direction from the origin to the point 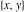 . .
Comparing the cotangent definition with the definitions of the sine and cosine functions shows that the following formula can also be used as a definition of the cotangent function:
A quick look at the cotangent function Here is a graphic of the cotangent function 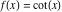 for real values of its argument for real values of its argument  . .
Representation through more general functions
The cotangent function  can be represented using more general mathematical functions. As the ratio of the cosine and sine functions that are particular cases of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the cotangent function can also be represented as ratios of those special functions. But these representations are not very useful. It is more useful to write the cotangent function as particular cases of one special function. That can be done using doubly periodic Jacobi elliptic functions that degenerate into the cotangent function when their second parameter is equal to can be represented using more general mathematical functions. As the ratio of the cosine and sine functions that are particular cases of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the cotangent function can also be represented as ratios of those special functions. But these representations are not very useful. It is more useful to write the cotangent function as particular cases of one special function. That can be done using doubly periodic Jacobi elliptic functions that degenerate into the cotangent function when their second parameter is equal to 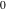 or or 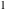 . .
Definition of the cotangent function for a complex argument In the complex  ‐plane, the function ‐plane, the function 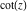 is defined using is defined using 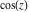 and and 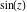 or the exponential function or the exponential function 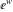 in the points in the points 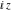 and and  through the formula: through the formula: In the points 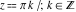 , where , where 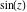 has zeros, the denominator of the last formula equals zero and has zeros, the denominator of the last formula equals zero and 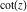 has singularities (poles of the first order). has singularities (poles of the first order). Here are two graphics showing the real and imaginary parts of the cotangent function over the complex plane.
The best-known properties and formulas for the cotangent function
Values in points
Students usually learn the following basic table of values of the cotangent function for special points of the circle:
General characteristics
For real values of argument  , the values of , the values of 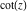 are real. are real.
In the points 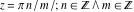 , the values of , the values of  are algebraic. In several cases they can be integers are algebraic. In several cases they can be integers 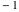 , 0, or 1: , 0, or 1:
The values of 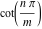 can be expressed using only square roots if can be expressed using only square roots if 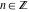 and and  is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}. is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}.
The function 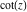 is an analytical function of is an analytical function of 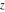 that is defined over the whole complex that is defined over the whole complex  ‐plane and does not have branch cuts and branch points. It has an infinite set of singular points: ‐plane and does not have branch cuts and branch points. It has an infinite set of singular points:
(a) 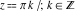 are the simple poles with residues are the simple poles with residues  .
(b) .
(b) 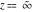 is an essential singular point. is an essential singular point.
It is a periodic function with the real period 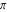 : :
The function 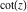 is an odd function with mirror symmetry: is an odd function with mirror symmetry:
Differentiation
The first derivative of 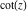 has simple representations using either the has simple representations using either the  function or the function or the 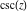 function: function:
The 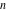 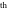 derivative of derivative of 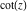 has much more complicated representations than symbolic has much more complicated representations than symbolic 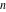  derivatives for derivatives for 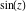 and and 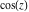 : :
where 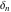 is the Kronecker delta symbol: is the Kronecker delta symbol: 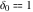 and and  . .
Ordinary differential equation
The function 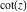 satisfies the following first-order nonlinear differential equation: satisfies the following first-order nonlinear differential equation:
Series representation
The function 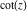 has a simple Laurent series expansion at the origin that converges for all finite values has a simple Laurent series expansion at the origin that converges for all finite values 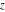 with with  : :
where 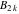 are the Bernoulli numbers. are the Bernoulli numbers.
Integral representation
The function  has a well-known integral representation through the following definite integral along the positive part of the real axis: has a well-known integral representation through the following definite integral along the positive part of the real axis:
Continued fraction representations
The function 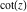 has the following simple continued fraction representation: has the following simple continued fraction representation:
Indefinite integration
Indefinite integrals of expressions that contain the cotangent function can sometimes be expressed using elementary functions. However, special functions are frequently needed to express the results even when the integrands have a simple form (if they can be evaluated in closed form). Here are some examples:
Definite integration
Definite integrals that contain the cotangent function are sometimes simple. For example, the famous Catalan constant 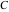 can be defined as the value of the following integral: can be defined as the value of the following integral:
This constant also appears in the following integral:
Some special functions can be used to evaluate more complicated definite integrals. For example, to express the following integral, the Gauss hypergeometric function is needed:
Finite summation
The following finite sum that contains a cotangent function can be expressed in terms of a cotangent function:
Other finite sums that contain a cotangent function can be expressed in terms of a polynomial function:
Infinite summation
The following infinite sum that contains the cotangent function has a very simple value:
Finite products
The following finite product from the cotangent has a very simple value:
Addition formulas
The cotangent of a sum can be represented by the rule: "the cotangent of a sum is equal to the product of the cotangents minus one divided by a sum of the cotangents." A similar rule is valid for the cotangent of the difference:
Multiple arguments
In the case of multiple arguments 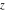 , ,  , , 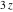 , …, the function , …, the function 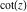 can be represented as the ratio of the finite sums that contains powers of cotangents: can be represented as the ratio of the finite sums that contains powers of cotangents:
Half-angle formulas
The cotangent of a half‐angle can be represented using two trigonometric functions by the following simple formulas:
The sine function in the last formula can be replaced by the cosine function. But it leads to a more complicated representation that is valid in some vertical strip:
To make this formula correct for all complex 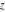 , a complicated prefactor is needed: , a complicated prefactor is needed:
where 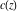 contains the unit step, real part, imaginary part, the floor, and the round functions. contains the unit step, real part, imaginary part, the floor, and the round functions.
Sums of two direct functions
The sum of two cotangent functions can be described by the rule: "the sum of cotangents is equal to the sine of the sum multiplied by the cosecants." A similar rule is valid for the difference of two cotangents:
Products involving the direct function
The product of two cotangents and the product of the cotangent and tangent have the following representations:
Inequalities
The most famous inequality for the cotangent function is the following:
Relations with its inverse function
There are simple relations between the function 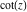 and its inverse function and its inverse function  : :
The second formula is valid at least in the vertical strip 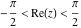 . Outside of this strip a much more complicated relation (that contains the unit step, real part, and the floor functions) holds: . Outside of this strip a much more complicated relation (that contains the unit step, real part, and the floor functions) holds:
Representations through other trigonometric functions
Cotangent and tangent functions are connected by a very simple formula that contains the linear function in the following argument:
The cotangent function can also be represented using other trigonometric functions by the following formulas:
Representations through hyperbolic functions
The cotangent function has representations using the hyperbolic functions:
Applications
The cotangent function is used throughout mathematics, the exact sciences, and engineering.
|