|
Introduction to the Cotangent Function in Mathematica
Overview
The following shows how the cotangent function is realized in Mathematica. Examples of evaluating Mathematica functions applied to various numeric and exact expressions that involve the cotangent function or return it are shown. These involve numeric and symbolic calculations and plots.
Notations
Mathematica forms of notations
Following Mathematica's general naming convention, function names in StandardForm are just the capitalized versions of their traditional mathematics names. This shows the cotangent function in StandardForm.
This shows the cotangent function in TraditionalForm.
Additional forms of notations
Mathematica has other popular forms of notations that are used for print and electronic publication. In this particular instance the task is not difficult. However, it must be made to work in Mathematica's CForm, TeXForm, and FortranForm.
Automatic evaluations and transformations
Evaluation for exact and machine-number values of arguments
For the exact argument 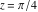 , Mathematica returns an exact result. , Mathematica returns an exact result.
For a machine‐number argument (numerical argument with a decimal point), a machine number is also returned.
The next inputs calculate 100‐digit approximations at 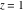 and and 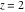 . .
Within a second, it is possible to calculate thousands of digits for the cotangent function. The next input calculates 10000 digits for 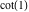 and analyzes the frequency of the digit and analyzes the frequency of the digit 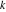 in the resulting decimal number. in the resulting decimal number.
Here is a 50‐digit approximation to the cotangent function at the complex argument 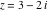 . .
Mathematica automatically evaluates mathematical functions with machine precision, if the arguments of the function are numerical values and include machine‐number elements. In this case only six digits after the decimal point are shown in the results. The remaining digits are suppressed, but can be displayed using the function InputForm.
Simplification of the argument
Mathematica knows the symmetry and periodicity of the cotangent function. Here are some examples.
Mathematica automatically simplifies the composition of the direct and the inverse cotangent functions into its argument.
Mathematica also automatically simplifies the composition of the direct and any of the inverse trigonometric functions into algebraic functions of the argument.
In the cases where the argument has the structure 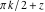 or or 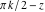 , and , and 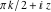 or or 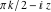 with integer with integer 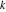 , the cotangent function can be automatically transformed into trigonometric or hyperbolic cotangent or tangent functions. , the cotangent function can be automatically transformed into trigonometric or hyperbolic cotangent or tangent functions.
Simplification of combinations of cotangent functions
Sometimes simple arithmetic operations containing the cotangent function can automatically generate other equal trigonometric functions.
The cotangent function arising as special cases from more general functions
The cotangent function can be treated as a particular case of some more general special functions. For example, 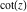 appears automatically from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions for appropriate values of their parameters. appears automatically from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions for appropriate values of their parameters.
Equivalence transformations using specialized Mathematica functions
General remarks
Almost everybody prefers using 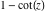 instead of instead of 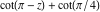 . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can result in overly complicated results. Compact expressions like . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can result in overly complicated results. Compact expressions like 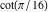 should not be automatically expanded into the more complicated expression should not be automatically expanded into the more complicated expression 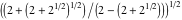 . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section. . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section.
TrigExpand
The function TrigExpand expands out trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in arguments of trigonometric and hyperbolic functions, and then expands out products of trigonometric and hyperbolic functions into sums of powers, using trigonometric and hyperbolic identities where possible. Here are some examples.
TrigFactor
The function TrigFactor factors trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in the arguments of trigonometric and hyperbolic functions, and then factors the resulting polynomials into trigonometric and hyperbolic functions, using trigonometric and hyperbolic identities where possible. Here are some examples.
TrigReduce
The function TrigReduce rewrites the products and powers of trigonometric and hyperbolic functions in terms of trigonometric and hyperbolic functions with combined arguments. In more detail, it typically yields a linear expression involving trigonometric and hyperbolic functions with more complicated arguments. TrigReduce is approximately opposite to TrigExpand and TrigFactor. Here are some examples.
TrigToExp
The function TrigToExp converts trigonometric and hyperbolic functions to exponentials. It tries, where possible, to give results that do not involve explicit complex numbers. Here are some examples.
ExpToTrig
The function ExpToTrig converts exponentials to trigonometric and hyperbolic functions. It is approximately opposite to TrigToExp. Here are some examples.
ComplexExpand
The function ComplexExpand expands expressions assuming that all the variables are real. The option TargetFunctions can be given as a list of functions from the set {Re, Im, Abs, Arg, Conjugate, Sign}. ComplexExpand tries to give results in terms of the functions specified. Here are some examples.
Simplify
The function Simplify performs a sequence of algebraic transformations on the expression, and returns the simplest form it finds. Here are some examples.
Here is a collection of trigonometric identities. Each is written as a logical conjunction.
The function Simplify has the Assumption option. For example, Mathematica treats the periodicity of trigonometric functions for the symbolic integer coefficient 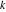 of of 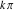 . .
Mathematica also knows that the composition of the inverse and direct trigonometric functions produces the value of the internal argument under the corresponding restriction.
FunctionExpand (and Together)
While the cotangent function auto‐evaluates for simple fractions of 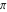 , for more complicated cases it stays as a cotangent function to avoid the build up of large expressions. Using the function FunctionExpand, the cotangent function can sometimes be transformed into explicit radicals. Here are some examples. , for more complicated cases it stays as a cotangent function to avoid the build up of large expressions. Using the function FunctionExpand, the cotangent function can sometimes be transformed into explicit radicals. Here are some examples.
If the denominator contains squares of integers other than 2, the results always contain complex numbers (meaning that the imaginary number 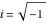 appears unavoidably). appears unavoidably).
Here the function RootReduce is used to express the previous algebraic numbers as roots of polynomial equations.
The function FunctionExpand also reduces trigonometric expressions with compound arguments or compositions, including inverse trigonometric functions, to simpler ones. Here are some examples.
Applying Simplify to the last expression gives a more compact result.
FullSimplify
The function FullSimplify tries a wider range of transformations than Simplify and returns the simplest form it finds. Here are some examples that contrast the results of applying these functions to the same expressions.
Operations under special Mathematica functions Series expansions Calculating the series expansion of a cotangent function to hundreds of terms can be done in seconds. Mathematica comes with the add‐on package DiscreteMath`RSolve` that allows finding the general terms of the series for many functions. After loading this package, and using the package function SeriesTerm, the following 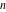 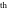 term of term of 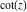 can be evaluated. can be evaluated. This result can be verified by the following process. Differentiation Mathematica can evaluate derivatives of the cotangent function of an arbitrary positive integer order. Finite products Mathematica can calculate some finite symbolic products that contain the cotangent function. Here is an example. Indefinite integration Mathematica can calculate a huge number of doable indefinite integrals that contain the cotangent function. The results can contain special functions. Here are some examples. Definite integration Mathematica can calculate wide classes of definite integrals that contain the cotangent function. Here are some examples. Limit operation Mathematica can calculate limits that contain the cotangent function. Here are some examples. Solving equations The next inputs solve two equations that contain the cotangent function. Because of the multivalued nature of the inverse cotangent function, a printed message indicates that only some of the possible solutions are returned. A complete solution of the previous equation can be obtained using the function Reduce. Solving differential equations Here is a nonlinear differential equation whose independent solutions include the cotangent function. In carrying out the algorithm to solve the following nonlinear differential equation, Mathematica has to solve a transcendental equation. In doing so, the generically multivariate inverse of a function is encountered, and a message is issued that a solution branch is potentially missed. Plotting Mathematica has built‐in functions for 2D and 3D graphics. Here are some examples.
|