|
Operations under special Mathematica functions Series expansions Calculating the series expansion of a hyperbolic cotangent function to hundreds of terms can be done in seconds. Mathematica comes with the add‐on package DiscreteMath`RSolve` that allows finding the general terms of the series for many functions. After loading this package, and using the package function SeriesTerm, the following 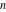 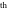 term of term of 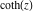 can be evaluated. can be evaluated. This result can be easily verified. Differentiation Mathematica can evaluate derivatives of the hyperbolic cotangent function of an arbitrary positive integer order. Indefinite integration Mathematica can calculate a huge set of doable indefinite integrals that contain the hyperbolic cotangent function. The results can contain special functions. Here are some examples. Definite integration Mathematica can calculate wide classes of definite integrals that contain the hyperbolic cotangent function. Here are some examples. Limit operation Mathematica can calculate limits that contain the hyperbolic cotangent function. Here are some examples. Solving equations The next inputs solve two equations that contain the hyperbolic cotangent function. Because of the multivalued nature of the inverse hyperbolic cotangent function, a message is printed indicating that only some of the possible solutions are returned. A complete solution of the previous equation can be obtained using the function Reduce. Solving differential equations Here is a linear inhomogeneous differential equation whose independent solution includes the hyperbolic tangent function. Here is a nonlinear differential equation whose solution is the hyperbolic tangent function with a shifted argument. Plotting Mathematica has built‐in functions for 2D and 3D graphics. Here are some examples.
|