|
The trigonometric functions are particular cases of more general functions. Among these more general functions, four different classes of special functions are particularly relevant: Bessel, Jacobi, Mathieu, and hypergeometric functions.
For example, 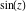 and and 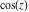 have the following representations through Bessel, Mathieu, and hypergeometric functions: have the following representations through Bessel, Mathieu, and hypergeometric functions:
On the other hand, all trigonometric functions can be represented as degenerate cases of the corresponding doubly periodic Jacobi elliptic functions when their second parameter is equal to 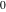 or or 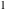 : :
Each of the six trigonometric functions can be represented through the corresponding hyperbolic function:
Each of the six trigonometric functions is connected with its corresponding inverse trigonometric function by two formulas. One is a simple formula, and the other is much more complicated because of the multivalued nature of the inverse function:
Each of the six trigonometric functions can be represented by any other trigonometric function as a rational function of that function with linear arguments. For example, the sine function can be representative as a group‐defining function because the other five functions can be expressed as follows:
All six trigonometric functions can be transformed into any other trigonometric function of this group if the argument 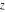 is replaced by is replaced by 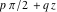 with with 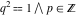 : :
|