|
Automatic evaluations and transformations
Evaluation for exact, machine-number, and high-precision arguments
For a simple exact argument, Mathematica returns exact results. For instance, for the argument 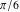 , the Sin function evaluates to , the Sin function evaluates to 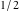 . .
For a generic machine‐number argument (a numerical argument with a decimal point and not too many digits), a machine number is returned.
The next inputs calculate 100‐digit approximations of the six trigonometric functions at 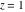 . .
Within a second, it is possible to calculate thousands of digits for the trigonometric functions. The next input calculates 10000 digits for 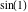 , ,  , , 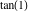 , , 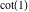 , , 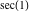 , and , and  and analyzes the frequency of the occurrence of the digit and analyzes the frequency of the occurrence of the digit 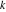 in the resulting decimal number. in the resulting decimal number.
Here are 50‐digit approximations to the six trigonometric functions at the complex argument 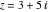 . .
Mathematica always evaluates mathematical functions with machine precision, if the arguments are machine numbers. In this case, only six digits after the decimal point are shown in the results. The remaining digits are suppressed, but can be displayed using the function InputForm.
Simplification of the argument
Mathematica uses symmetries and periodicities of all the trigonometric functions to simplify expressions. Here are some examples.
Mathematica automatically simplifies the composition of the direct and the inverse trigonometric functions into the argument.
Mathematica also automatically simplifies the composition of the direct and any of the inverse trigonometric functions into algebraic functions of the argument.
In cases where the argument has the structure 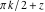 or or 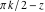 , and , and 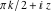 or or 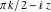 with integer with integer 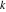 , trigonometric functions can be automatically transformed into other trigonometric or hyperbolic functions. Here are some examples. , trigonometric functions can be automatically transformed into other trigonometric or hyperbolic functions. Here are some examples.
Simplification of simple expressions containing trigonometric functions
Sometimes simple arithmetic operations containing trigonometric functions can automatically produce other trigonometric functions.
Trigonometric functions arising as special cases from more general functions
All trigonometric functions can be treated as particular cases of some more advanced special functions. For example, 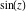 and and 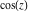 are sometimes the results of auto-simplifications from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions (for appropriate values of their parameters). are sometimes the results of auto-simplifications from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions (for appropriate values of their parameters).
|