|
Connections within the group of trigonometric functions and with other function groups
Representations through more general functions
The trigonometric functions are particular cases of more general functions. Among these more general functions, four different classes of special functions are particularly relevant: Bessel, Jacobi, Mathieu, and hypergeometric functions.
For example,  and and  have the following representations through Bessel, Mathieu, and hypergeometric functions: have the following representations through Bessel, Mathieu, and hypergeometric functions:
On the other hand, all trigonometric functions can be represented as degenerate cases of the corresponding doubly periodic Jacobi elliptic functions when their second parameter is equal to 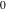 or or 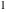 : :
Representations through related equivalent functions
Each of the six trigonometric functions can be represented through the corresponding hyperbolic function:
Relations to inverse functions
Each of the six trigonometric functions is connected with its corresponding inverse trigonometric function by two formulas. One is a simple formula, and the other is much more complicated because of the multivalued nature of the inverse function:
Representations through other trigonometric functions
Each of the six trigonometric functions can be represented by any other trigonometric function as a rational function of that function with linear arguments. For example, the sine function can be representative as a group‐defining function because the other five functions can be expressed as follows:
All six trigonometric functions can be transformed into any other trigonometric function of this group if the argument 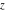 is replaced by is replaced by 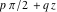 with with 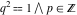 : :
|