|
Introduction to the hyperbolic functions
General
The six well‐known hyperbolic functions are the hyperbolic sine 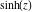 , hyperbolic cosine , hyperbolic cosine 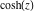 , hyperbolic tangent , hyperbolic tangent 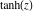 , hyperbolic cotangent , hyperbolic cotangent 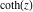 , hyperbolic cosecant , hyperbolic cosecant 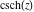 , and hyperbolic secant , and hyperbolic secant  . They are among the most used elementary functions. The hyperbolic functions share many common properties and they have many properties and formulas that are similar to those of the trigonometric functions. . They are among the most used elementary functions. The hyperbolic functions share many common properties and they have many properties and formulas that are similar to those of the trigonometric functions.
Definitions of the hyperbolic functions
All hyperbolic functions can be defined as simple rational functions of the exponential function of 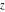 : :
The functions 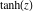 , ,  , , 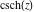 , and , and  can also be defined through the functions can also be defined through the functions 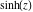 and and 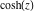 using the following formulas: using the following formulas:
A quick look at the hyperbolic functions Here is a quick look at the graphics of the six hyperbolic functions along the real axis.
Connections within the group of hyperbolic functions and with other function groups
Representations through more general functions
The hyperbolic functions are particular cases of more general functions. Among these more general functions, four classes of special functions are of special relevance: Bessel, Jacobi, Mathieu, and hypergeometric functions.
For example, 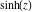 and and 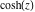 have the following representations through Bessel, Mathieu, and hypergeometric functions: have the following representations through Bessel, Mathieu, and hypergeometric functions:
All hyperbolic functions can be represented as degenerate cases of the corresponding doubly periodic Jacobi elliptic functions when their second parameter is equal to 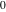 or or 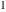 : :
Representations through related equivalent functions
Each of the six hyperbolic functions can be represented through the corresponding trigonometric function:
Relations to inverse functions
Each of the six hyperbolic functions is connected with a corresponding inverse hyperbolic function by two formulas. One direction can be expressed through a simple formula, but the other direction is much more complicated because of the multivalued nature of the inverse function:
Representations through other hyperbolic functions
Each of the six hyperbolic functions can be represented through any other function as a rational function of that function with a linear argument. For example, the hyperbolic sine can be representative as a group‐defining function because the other five functions can be expressed as:
All six hyperbolic functions can be transformed into any other function of the group of hyperbolic functions if the argument 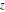 is replaced by is replaced by 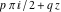 with with 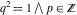 : :
The best-known properties and formulas for hyperbolic functions
Real values for real arguments
For real values of argument  , the values of all the hyperbolic functions are real (or infinity). , the values of all the hyperbolic functions are real (or infinity).
In the points 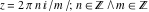 , the values of the hyperbolic functions are algebraic. In several cases, they can even be rational numbers, , the values of the hyperbolic functions are algebraic. In several cases, they can even be rational numbers,  , or , or  (e.g. (e.g. 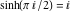 , , 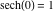 , or , or 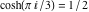 ). They can be expressed using only square roots if ). They can be expressed using only square roots if 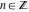 and and 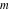 is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}. is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}.
Simple values at zero
All hyperbolic functions has rather simple values for arguments 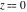 and and 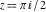 : :
Analyticity
All hyperbolic functions are defined for all complex values of  , and they are analytical functions of , and they are analytical functions of  over the whole complex over the whole complex  ‐plane and do not have branch cuts or branch points. The two functions ‐plane and do not have branch cuts or branch points. The two functions 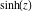 and and 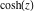 are entire functions with an essential singular point at are entire functions with an essential singular point at  . All other hyperbolic functions are meromorphic functions with simple poles at points . All other hyperbolic functions are meromorphic functions with simple poles at points 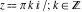 (for (for  and and 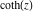 ) and at points ) and at points 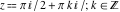 (for (for 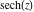 and and 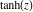 ). ).
Periodicity
All hyperbolic functions are periodic functions with a real period (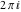 or or 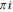 ): ):
Parity and symmetry
All hyperbolic functions have parity (either odd or even) and mirror symmetry:
Simple representations of derivatives
The derivatives of all hyperbolic functions have simple representations that can be expressed through other hyperbolic functions:
Simple differential equations
The solutions of the simplest second‐order linear ordinary differential equation with constant coefficients can be represented through 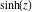 and and 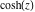 . The other hyperbolic functions satisfy first‐order nonlinear differential equations: . The other hyperbolic functions satisfy first‐order nonlinear differential equations:
All six hyperbolic functions satisfy first‐order nonlinear differential equations:
Applications of hyperbolic functions
Trigonometric functions are intimately related to triangle geometry. Functions like sine and cosine are often introduced as edge lengths of right‐angled triangles. Hyperbolic functions occur in the theory of triangles in hyperbolic spaces.
Lobachevsky (1829) and J. Bolyai (1832) independently recognized that Euclid's fifth postulate—saying that for a given line and a point not on the line, there is exactly one line parallel to the first—might be changed and still be a consistent geometry. In the hyperbolic geometry it is allowable for more than one line to be parallel to the first (meaning that the parallel lines will never meet the first, however far they are extended). Translated into triangles, this means that the sum of the three angles is always less than 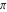 . .
A particularly nice representation of the hyperbolic geometry can be realized in the unit disk of complex numbers (the Poincaré disk model). In this model, points are complex numbers in the unit disk, and the lines are either arcs of circles that meet the boundary of the unit circle orthogonal or diameters of the unit circle.
The distance 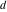 between two points (meaning complex numbers) between two points (meaning complex numbers)  and and 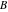 in the Poincaré disk is: in the Poincaré disk is:
The attractive feature of the Poincaré disk model is that the hyperbolic angles agree with the Euclidean angles. Formally, the angle 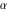 at a point at a point 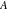 of two hyperbolic lines of two hyperbolic lines 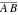 and and 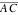 is described by the formula: is described by the formula:
In the following, the values of the three angles of an hyperbolic triangle at the vertices 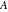 , , 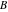 , and , and 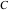 are denoted through are denoted through 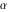 , , 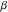 , and , and 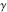 . The hyperbolic length of the three edges opposite to the angles are denoted . The hyperbolic length of the three edges opposite to the angles are denoted 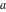 , , 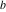 , and , and 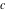 . .
The cosine rule and the second cosine rule for hyperbolic triangles are:
The sine rule for hyperbolic triangles is:
For a right‐angle triangle, the hyperbolic version of the Pythagorean theorem follows from the preceding formulas (the right angle is taken at vertex  ): ):
Using the series expansion 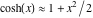 at small scales the hyperbolic geometry is approximated by the familar Euclidean geometry. The cosine formulas and the sine formulas for hyperbolic triangles with a right angle at vertex at small scales the hyperbolic geometry is approximated by the familar Euclidean geometry. The cosine formulas and the sine formulas for hyperbolic triangles with a right angle at vertex 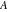 become: become:
The inscribed circle has the radius:
The circumscribed circle has the radius:
Other applications
As rational functions of the exponential function, the hyperbolic functions appear virtually everywhere in quantitative sciences. It is impossible to list their numerous applications in teaching, science, engineering, and art.
|