|
The hyperbolic secant function is an old mathematical function.
This function is easily defined as the ratio of one and hyperbolic cosine functions:
After comparison with the famous Euler formula for the cosine function 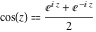 , it is easy to derive the following representation of the hyperbolic secant through the circular secant:
The previous formula allows establishment of all the properties and formulas for the hyperbolic secant from corresponding properties and formulas for the circular secant.
|
