|
Intrinsic curvature curves Curves with intrinsic curvature 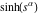 , with , with 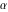 ranging from 0 (red) to 2 (violet). ranging from 0 (red) to 2 (violet). 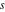 parametrizes the curve. parametrizes the curve. Intrinsic curvature-torsion curves Curves with intrinsic curvature  and intrinsic torsion and intrinsic torsion 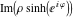 with with  ranging from 0 (red) to ranging from 0 (red) to 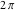 (violet). (violet). 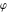 parametrizes each curve. parametrizes each curve. Phase portraits Phase portrait of the  function. The left graphic shows the curves function. The left graphic shows the curves 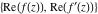 . The curves are parametrized by . The curves are parametrized by  with with 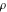 varying (dark red curves) and φ varying (yellow curves). The right graphic shows the curves varying (dark red curves) and φ varying (yellow curves). The right graphic shows the curves 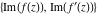 . The curves are parametrized by . The curves are parametrized by 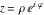 with with 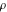 varying (dark blue curves) and φ varying (violet curves). varying (dark blue curves) and φ varying (violet curves). Generalized phase portrait of the 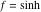 function. The left graphics shows the curves function. The left graphics shows the curves 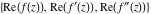 . The curves are parametrized by . The curves are parametrized by 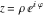 with with 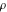 varying (dark red curves) and φ varying (yellow curves). The right graphics shows the curves varying (dark red curves) and φ varying (yellow curves). The right graphics shows the curves 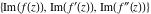 . The curves are parametrized by . The curves are parametrized by  with with 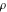 varying (dark blue curves) and φ varying (violet curves). varying (dark blue curves) and φ varying (violet curves). Offset curves Wavefront caustic of the function 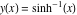 . The gray curve is the function . The gray curve is the function 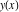 . The red lines are normals on this curve. The blue curves are the caustics formed by the normals. . The red lines are normals on this curve. The blue curves are the caustics formed by the normals. Pursuit curves Pursuit curves with respect to the function 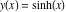 . The gray curve is the function . The gray curve is the function 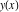 . The red curves are pursuit curves that start at different positions. . The red curves are pursuit curves that start at different positions. Evolute Evolute and osculating circles of the function 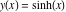 . The gray curve is the function . The gray curve is the function  . The osculating circles are colored according to their radius and the blue curve is the evolute. The green lines connect the centers of the osculating circles with the points where the circles touch the curve. . The osculating circles are colored according to their radius and the blue curve is the evolute. The green lines connect the centers of the osculating circles with the points where the circles touch the curve. Involutes Involutes of the function 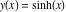 . The gray curve is the function . The gray curve is the function 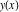 . The involutes are shown as red curves. . The involutes are shown as red curves. Pedal curves Family of pedal curves of the function 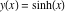 . . Family of contrapedal curves of the function 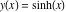 . . Wavefront caustic surfaces Wavefront caustics of the real part and the imaginary part of the function 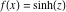 . The upper two graphics show the two wavefront caustic surfaces of the real part and the lower two graphics show the two wavefront caustic surfaces of the imaginary part. . The upper two graphics show the two wavefront caustic surfaces of the real part and the lower two graphics show the two wavefront caustic surfaces of the imaginary part.
|