|
Representation through more general functions
The tangent function 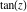 can be represented using more general mathematical functions. As the ratio of the sine and cosine functions that are particular cases of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the tangent function can also be represented as ratios of those special functions. But these representations are not very useful. It is more useful to write the tangent function as particular cases of one special function. That can be done using doubly periodic Jacobi elliptic functions that degenerate into the tangent function when their second parameter is equal to can be represented using more general mathematical functions. As the ratio of the sine and cosine functions that are particular cases of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the tangent function can also be represented as ratios of those special functions. But these representations are not very useful. It is more useful to write the tangent function as particular cases of one special function. That can be done using doubly periodic Jacobi elliptic functions that degenerate into the tangent function when their second parameter is equal to 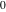 or or  : :
|