|
Definition of the tangent function for a complex argument In the complex 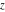 ‐plane, the function ‐plane, the function 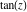 is defined using is defined using 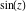 and and  or the exponential function or the exponential function 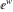 in the points in the points 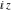 and and  through the formula: through the formula: In the points  , where , where 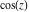 has zeros, the denominator of the last formula equals zero and has zeros, the denominator of the last formula equals zero and 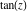 has singularities (poles of the first order). has singularities (poles of the first order). Here are two graphics showing the real and imaginary parts of the tangent function over the complex plane.
|