|
Introduction to the Tangent Function in Mathematica
Overview
The following shows how the tangent function is realized in Mathematica. Examples of evaluating Mathematica functions applied to various numeric and exact expressions that involve the tangent function or return it are shown. These involve numeric and symbolic calculations and plots.
Notations
Mathematica forms of notations
Following Mathematica's general naming convention, function names in StandardForm are just the capitalized versions of their traditional mathematics names. This shows the tangent function in StandardForm.
This shows the tangent function in TraditionalForm.
Additional forms of notations
Mathematica also knows the most popular forms of notations for the tangent function that are used in other programming languages. Here are three examples: CForm, TeXForm, and FortranForm.
Automatic evaluations and transformations
Evaluation for exact, machine-number, and high-precision arguments
For the exact argument 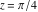 , Mathematica returns an exact result. , Mathematica returns an exact result.
For a machine‐number argument (a numerical argument with a decimal point and not too many digits), a machine number is also returned.
The next inputs calculate 100‐digit approximations at 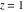 and and 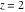 . .
Within a second, it is possible to calculate thousands of digits for the tangent function. The next input calculates 10000 digits for 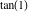 and analyzes the frequency of the digit and analyzes the frequency of the digit 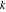 in the resulting decimal number. in the resulting decimal number.
Here is a 50‐digit approximation of the tangent function at the complex argument 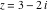 . .
Mathematica automatically evaluates mathematical functions with machine precision, if the arguments of the function are machine‐number elements. In this case, only six digits after the decimal point are shown in the results. The remaining digits are suppressed, but can be displayed using the function InputForm.
Simplification of the argument
Mathematica knows symmetry and periodicity of the tangent function. Here are some examples.
Mathematica automatically simplifies the composition of the direct and the inverse tangent functions into its argument.
Mathematica also automatically simplifies the composition of the direct and any of the inverse trigonometric functions into algebraic functions of the argument.
If the argument has the structure 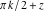 or or  , and , and  or or 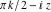 with integer with integer 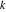 , the tangent function can be automatically transformed into trigonometric or hyperbolic tangent or cotangent functions. , the tangent function can be automatically transformed into trigonometric or hyperbolic tangent or cotangent functions.
Simplification of simple expressions containing the tangent function
Sometimes simple arithmetic operations containing the tangent function can automatically produce other trigonometric functions.
The tangent function arising as special cases from more general functions
The tangent function can be treated as a particular case of some more general special functions. For example, 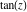 can appear automatically from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions for appropriate values of their parameters. can appear automatically from Bessel, Mathieu, Jacobi, hypergeometric, and Meijer functions for appropriate values of their parameters.
Equivalence transformations carried out by specialized Mathematica functions
General remarks
Almost everybody prefers using 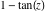 instead of instead of 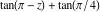 . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can give overly complicated results. Compact expressions like . Mathematica automatically transforms the second expression into the first one. The automatic application of transformation rules to mathematical expressions can give overly complicated results. Compact expressions like  should not be automatically expanded into the more complicated expression should not be automatically expanded into the more complicated expression 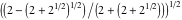 . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section. . Mathematica has special functions that produce such expansions. Some are demonstrated in the next section.
TrigExpand
The function TrigExpand expands out trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in the arguments of trigonometric and hyperbolic functions, and then expands out the products of trigonometric and hyperbolic functions into sums of powers, using trigonometric and hyperbolic identities where possible. Here are some examples.
TrigFactor
The function TrigFactor factors trigonometric and hyperbolic functions. In more detail, it splits up sums and integer multiples that appear in the arguments of trigonometric and hyperbolic functions, and then factors the resulting polynomials into trigonometric and hyperbolic functions, using trigonometric and hyperbolic identities where possible. Here are some examples.
TrigReduce
The function TrigReduce rewrites products and powers of trigonometric and hyperbolic functions in terms of trigonometric and hyperbolic functions with combined arguments. In more detail, it typically yields a linear expression involving trigonometric and hyperbolic functions with more complicated arguments. TrigReduce is approximately opposite to TrigExpand and TrigFactor. Here are some examples.
TrigToExp
The function TrigToExp converts trigonometric and hyperbolic functions to exponentials. It tries, where possible, to give results that do not involve explicit complex numbers. Here are some examples.
ExpToTrig
The function ExpToTrig converts exponentials to trigonometric and hyperbolic functions. It is approximately inverse to TrigToExp. Here are some examples.
ComplexExpand
The function ComplexExpand expands expressions assuming that all the variables are real. The value option TargetFunctions is a list of functions from the set {Re, Im, Abs, Arg, Conjugate, Sign}. ComplexExpand tries to give results in terms of the functions specified. Here are some examples.
Simplify
The function Simplify performs a sequence of algebraic transformations on the expression, and returns the simplest form it finds. Here are some examples.
Here is a collection of trigonometric identities. All are written as one large logical conjunction.
The function Simplify has the Assumption option. For example, Mathematica treats the periodicity of trigonometric functions for the symbolic integer coefficient 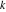 of of 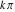 . .
Mathematica also knows that the composition of the inverse and the direct trigonometric functions produces the value of the internal argument under the corresponding restriction.
FunctionExpand (and Together)
While the tangent function auto‐evaluates for simple fractions of 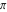 , for more complicated cases it stays as a tangent function to avoid the build up of large expressions. Using the function FunctionExpand, the tangent function can sometimes be transformed into explicit radicals. Here are some examples. , for more complicated cases it stays as a tangent function to avoid the build up of large expressions. Using the function FunctionExpand, the tangent function can sometimes be transformed into explicit radicals. Here are some examples.
If the denominator contains squares of integers other than 2, the results always contain complex numbers (meaning that the imaginary number 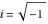 appears unavoidably). appears unavoidably).
Here the function RootReduce is used to express the previous algebraic numbers as roots of polynomial equations.
The function FunctionExpand also reduces trigonometric expressions with compound arguments or compositions, including inverse trigonometric functions, to simpler ones. Here are some examples.
Applying Simplify to the previous expression gives a more compact result.
FullSimplify
The function FullSimplify tries a wider range of transformations than Simplify and returns the simplest form it finds. Here are some examples that contrast the results of applying the functions Simplify and FullSimplify to the same expressions.
Operations carried out by specialized Mathematica functions Series expansions Calculating the series expansion of a tangent function to hundreds of terms can be done in seconds. Mathematica comes with the add‐on package DiscreteMath`RSolve` that allows finding the general terms of series for many functions. After loading this package, and using the package function SeriesTerm, the following 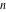 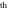 term of term of 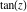 can be evaluated. can be evaluated. The result can be checked by the following process. Differentiation Mathematica can evaluate derivatives of the tangent function of an arbitrary positive integer order. Finite products Mathematica can calculate some finite symbolic products that contain the tangent function. Here is an example. Indefinite integration Mathematica can calculate a huge number of doable indefinite integrals that contain the tangent function. Here are some examples. Definite integration Mathematica can calculate wide classes of definite integrals that contain the tangent function. Here are some examples. Limit operation Mathematica can calculate limits that contain the tangent function. Here are some examples. Solving equations The next inputs solve two equations that contain the tangent function. Because of the multivalued nature of the inverse tangent function, a printed message indicates that only some of the possible solutions are returned. A complete solution of the previous equation can be obtained using the function Reduce. Solving differential equations Here is a nonlinear differential equation whose independent solutions include the tangent function. In the previous input, the differential equation was solved for 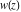 . If the argument is suppressed, the result is returned as a pure function (in the sense of the . If the argument is suppressed, the result is returned as a pure function (in the sense of the 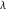 ‐calculus). ‐calculus). The advantage of such a pure function is that it can be used for different arguments, derivatives, and more. In carrying out the algorithm to solve the following nonlinear differential equation, Mathematica has to solve a transcendental equation. In doing so, the generically multivariate inverse of a function is encountered, and a message is issued that a solution branch is potentially missed. Plotting Mathematica has built‐in functions for 2D and 3D graphics. Here are some examples.
|