|
Introduction to to elliptic exp and elliptic log
General
The elliptic exp and elliptic log appeared in the article of D. Masser (1975). These functions and the derivative of elliptic exp were implemented in the technical computing software Mathematica as part of the implementation of numerous mathematical functions that were used for elliptic and number theory functions.
Definitions of the elliptic exp and elliptic log
The elliptic exponent  , its derivative , its derivative 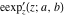 , and the elliptic logarithm , and the elliptic logarithm 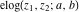 are defined by the following formulas: are defined by the following formulas:
A quick look at the elliptic exp and elliptic log Here is a quick look at the two components of the elliptic exponent and its derivative. All of the following graphics use the parameters 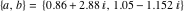 . The double periodicity of the function and the poles of order 2 to 4 are clearly visible. . The double periodicity of the function and the poles of order 2 to 4 are clearly visible. The last pair of graphics shows the elliptic logarithm over the complex  ‐plane. Compared with the direct function, it is relatively structureless. ‐plane. Compared with the direct function, it is relatively structureless.
Connections within the group of elliptic exp and elliptic log and with other function groups
Representations through more general functions
The elliptic logarithm 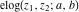 is the particular case of the hypergeometric function of two variables (Appell function is the particular case of the hypergeometric function of two variables (Appell function 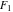 ): ):
Representations through related equivalent functions
The elliptic exponent 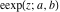 is connected with Jacobi amplitude by the following formula: is connected with Jacobi amplitude by the following formula:
The elliptic exponent 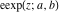 and elliptic logarithm and elliptic logarithm 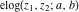 can be expressed through direct and inverse Weierstrass functions by the following formulas: can be expressed through direct and inverse Weierstrass functions by the following formulas:
The elliptic logarithm  has the following representation through incomplete elliptic integral has the following representation through incomplete elliptic integral 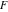 : :
Relations to inverse functions
The elliptic logarithm  is the inverse function to the elliptic exponent is the inverse function to the elliptic exponent 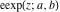 and its derivative and its derivative 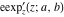 . Relations between them are described by the following formulas: . Relations between them are described by the following formulas:
The best-known properties and formulas for elliptic exp and elliptic log
Values at zero
The elliptic exponent  , its derivative , its derivative 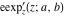 , and the elliptic logarithm , and the elliptic logarithm 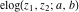 have the following values at the origin point: have the following values at the origin point:
Specific values for specialized parameter
The elliptic exponent 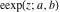 has the following value at the specialized point has the following value at the specialized point  : :
Analyticity
The elliptic exponent 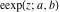 and its derivative and its derivative 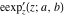 are vector‐valued functions of are vector‐valued functions of 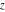 , , 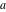 , and , and 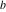 , which are analytic in each component, and they are defined over , which are analytic in each component, and they are defined over 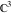 . .
The elliptic logarithm  is an analytical function of is an analytical function of 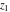 , ,  , , 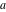 , , 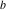 , which is defined in , which is defined in 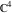 . .
The elliptic exponent 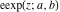 , its derivative , its derivative 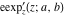 , and the elliptic logarithm , and the elliptic logarithm 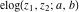 have complicated branch cuts. have complicated branch cuts.
Poles and essential singularities
The elliptic logarithm 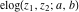 does not have poles and essential singularities. does not have poles and essential singularities.
Periodicity
The elliptic exponent 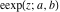 , its derivative , its derivative 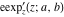 , and the elliptic logarithm , and the elliptic logarithm  do not have periodicity. do not have periodicity.
Parity and symmetry
The elliptic exponent 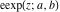 , its derivative , its derivative  , and the elliptic logarithm , and the elliptic logarithm 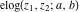 have mirror symmetry: have mirror symmetry:
Integral representations
The elliptic logarithm 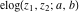 has the following integral representation: has the following integral representation:
Identities
The elliptic exponent 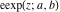 satisfies the following identities including the complete elliptic integral satisfies the following identities including the complete elliptic integral 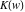 : :
Simple representations of derivatives
The first derivatives of elliptic exponent 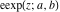 and the elliptic logarithm and the elliptic logarithm 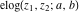 have the following representations: have the following representations:
Differential equations
The elliptic exponent 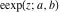 , its derivative , its derivative  , and the elliptic logarithm , and the elliptic logarithm 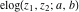 satisfy the following ordinary nonlinear differential equations: satisfy the following ordinary nonlinear differential equations:
Applications of the elliptic exp and elliptic log
Applications of the elliptic exponent 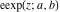 and elliptic logarithm and elliptic logarithm 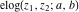 include number theory and solutions for the cubic and quartic Diophantine equations. include number theory and solutions for the cubic and quartic Diophantine equations.
|