|
Introduction to the Jacobi theta functions
General
The basic achievements in studying infinite series were made in the 18th and 19th centuries when mathematicians investigated issues regarding the convergence of different types of series. In particular, they found that the famous geometrical series:
converges inside the unit circle z < 1 to the function  , but can be analytically extended outside this circle by the formulas , but can be analytically extended outside this circle by the formulas  and and 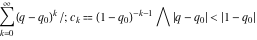 . The sums of these two series produce the same function . The sums of these two series produce the same function 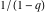 . But restrictions on convergence for all three series strongly depend on the distance between the center of expansion . But restrictions on convergence for all three series strongly depend on the distance between the center of expansion 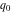 and the nearest singular point 1 (where the function and the nearest singular point 1 (where the function 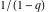 has a first-order pole). has a first-order pole).
The properties of the series:
lead to similar results, which attracted the interest of J. Bernoulli (1713), L. Euler, J. Fourier, and other researchers. They found that this series cannot be analytically continued outside the unit circle z < 1 because its boundary z ⩵ 1 has not one, but an infinite set of dense singular points. This boundary was called the natural boundary of analyticity of the corresponding function, which is defined as the sum of the previous series.
Special contributions to the theoretical development of these series were made by C. G. J. Jacobi (1827), who introduced the elliptic amplitude 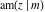 and studied the twelve elliptic functions and studied the twelve elliptic functions 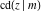 , , 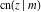 , , 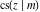 , , 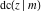 , , 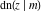 , , 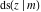 , , 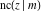 , , 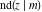 , ,  , , 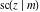 , , 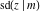 , , 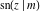 . All these functions later were named for Jacobi. C. G. J. Jacobi also introduced four basic theta functions, which can be expressed through the following series: . All these functions later were named for Jacobi. C. G. J. Jacobi also introduced four basic theta functions, which can be expressed through the following series:
These Jacobi elliptic theta functions notated by the symbols  , , 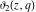 , , 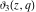 , and , and  have the following representations: have the following representations:
A more detailed theory of elliptic theta functions was developed by C. W. Borchardt (1838), K. Weierstrass (1862–1863), and others. Many relations in the theory of elliptic functions include derivatives of the theta functions with respect to the variable 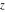 : : 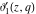 , , 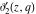 , ,  , and , and  , which cannot be expressed through other special functions. For this reason, Mathematica includes not only four well-known theta functions, but also their derivatives. , which cannot be expressed through other special functions. For this reason, Mathematica includes not only four well-known theta functions, but also their derivatives.
Definitions of Jacobi theta functions
The Jacobi elliptic theta functions 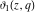 , , 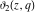 , , 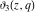 , and , and 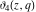 , and their derivatives with respect to , and their derivatives with respect to 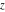 : : 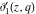 , , 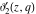 , , 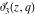 , and , and  are defined by the following formulas: are defined by the following formulas:
A quick look at the Jacobi theta functions Here is a quick look at the graphics for the Jacobi theta functions along the real axis for 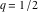 . .
Connections within the group of Jacobi theta functions and with other function groups
Representations through related equivalent functions
The elliptic theta functions 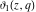 , , 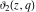 , , 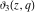 , and , and 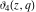 can be represented through the Weierstrass sigma functions by the following formulas: can be represented through the Weierstrass sigma functions by the following formulas:
where 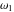 , , 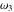 are the Weierstrass half-periods and are the Weierstrass half-periods and 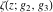 is the Weierstrass zeta function. is the Weierstrass zeta function.
The ratios of two different elliptic theta functions 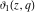 , , 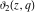 , ,  , and , and 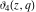 can be expressed through corresponding elliptic Jacobi functions with power factors by the following formulas: can be expressed through corresponding elliptic Jacobi functions with power factors by the following formulas:
where 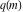 is an elliptic nome and is an elliptic nome and 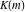 is a complete elliptic integral. is a complete elliptic integral.
Representations through other Jacobi theta functions
Each of the theta functions 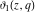 , , 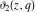 , , 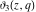 , and , and 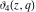 can be represented through the other theta functions by the following formulas: can be represented through the other theta functions by the following formulas:
The derivatives of the theta functions 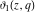 , , 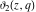 , ,  , and , and 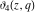 can also be expressed through the other theta functions and their derivatives by the following formulas: can also be expressed through the other theta functions and their derivatives by the following formulas:
The best-known properties and formulas for the Jacobi theta functions
Values for real arguments
For real values of the arguments 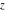 , ,  (with (with 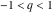 ), the values of the Jacobi theta functions ), the values of the Jacobi theta functions 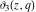 , ,  , , 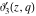 , and , and 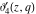 are real. are real.
For real values of the arguments 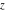 , , 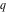 (with (with 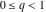 ), the values of the Jacobi theta functions ), the values of the Jacobi theta functions 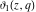 , , 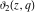 , ,  , and , and 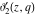 are real. are real.
Simple values at zero
All Jacobi theta functions 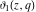 , , 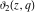 , ,  , ,  , , 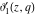 , , 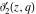 , , 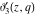 , and , and 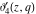 have the following simple values at the origin point: have the following simple values at the origin point:
Specific values for specialized parameter
All Jacobi theta functions 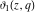 , ,  , , 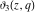 , ,  , ,  , , 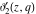 , , 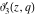 , and , and 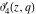 have the following simple values if have the following simple values if  : :
At the points 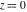 and and  , all theta functions , all theta functions 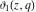 , , 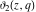 , , 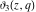 , ,  , , 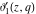 , , 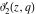 , , 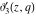 , and , and 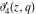 can be expressed through the Dedekind eta function can be expressed through the Dedekind eta function 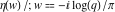 or a composition of the complete elliptic function or a composition of the complete elliptic function 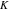 and the inverse elliptic nome and the inverse elliptic nome 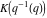 by the following formulas: by the following formulas:
The previous relations can be generalized for the cases  and and 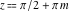 , where , where 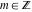 : :
Analyticity
All Jacobi theta functions 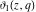 , , 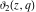 , , 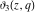 , , 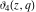 , , 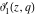 , , 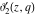 , , 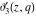 , and , and 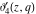 are analytic functions of are analytic functions of 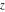 and and 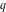 for for 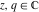 and and 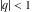 . .
Poles and essential singularities
All Jacobi theta functions 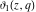 , , 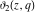 , ,  , , 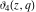 , , 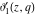 , , 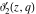 , ,  , and , and 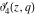 do not have poles and essential singularities inside of the unit circle do not have poles and essential singularities inside of the unit circle 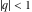 . .
Branch points and branch cuts
For fixed 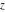 , the functions , the functions 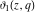 , , 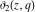 , , 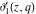 , and , and  have one branch point: have one branch point: 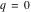 . (The point . (The point 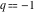 is the branch cut endpoint.) is the branch cut endpoint.)
For fixed 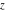 , the functions , the functions  , , 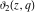 , , 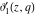 , and , and 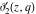 are the single‐valued functions inside the unit circle of the complex are the single‐valued functions inside the unit circle of the complex 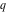 ‐plane, cut along the interval ‐plane, cut along the interval 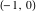 , where they are continuous from above: , where they are continuous from above:
For fixed 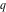 , the functions , the functions  , , 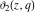 , , 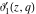 , and , and 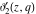 do not have branch points and branch cuts with respect to do not have branch points and branch cuts with respect to  . .
The functions 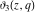 , , 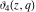 , , 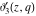 , and , and  do not have branch points and branch cuts. do not have branch points and branch cuts.
Natural boundary of analyticity
The unit circle 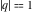 is the natural boundary of the region of analyticity for all Jacobi theta functions is the natural boundary of the region of analyticity for all Jacobi theta functions 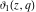 , , 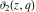 , , 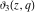 , , 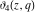 , , 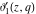 , , 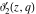 , ,  , and , and 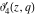 . .
Periodicity
The Jacobi theta functions 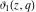 and and 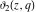 are the periodic functions with respect to are the periodic functions with respect to  with period with period 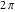 and a quasi‐period and a quasi‐period 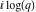 : :
The Jacobi theta functions 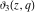 and and 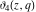 are the periodic functions with respect to are the periodic functions with respect to 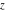 with period with period 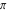 and a quasi‐period and a quasi‐period 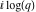 : :
The Jacobi theta functions 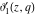 and and 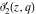 are the periodic functions with respect to are the periodic functions with respect to  with period with period 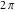 : :
The Jacobi theta functions 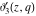 and and 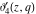 are the periodic functions with respect to are the periodic functions with respect to 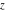 with period with period  : :
The previous formulas are the particular cases of the following general relations that reflect the periodicity and quasi‐periodicity of the theta functions by variable  : :
Parity and symmetry
All Jacobi theta functions 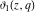 , , 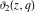 , , 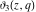 , , 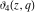 , , 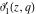 , , 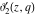 , , 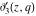 , and , and 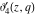 have mirror symmetry: have mirror symmetry:
The Jacobi theta functions 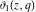 , , 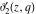 , , 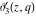 , and , and 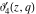 are odd functions with respect to are odd functions with respect to 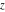 : :
The other Jacobi theta functions  , , 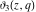 , , 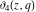 , and , and 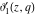 are even functions with respect to are even functions with respect to 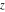 : :
The Jacobi theta functions 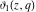 , , 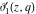 , , 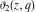 , and , and  satisfy the following parity type relations with respect to satisfy the following parity type relations with respect to 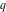 : :
The Jacobi theta functions 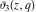 , ,  , , 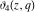 , and , and 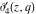 with argument with argument 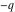 can be self-transformed by the following relations: can be self-transformed by the following relations:
q-series representations
All Jacobi elliptic theta functions 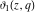 , , 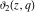 , , 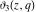 , and , and 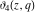 , and their derivatives , and their derivatives 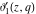 , , 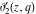 , , 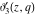 , and , and 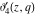 have the following series expansions, which can be called have the following series expansions, which can be called  ‐series representations: ‐series representations:
Other series representations
The theta functions 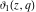 , , 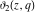 , , 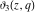 , and , and  , and their derivatives , and their derivatives 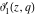 , , 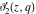 , ,  , and , and 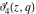 can also be represented through the following series: can also be represented through the following series:
Product representations
The theta functions can be represented through infinite products, for example:
Transformations
The theta functions 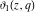 , , 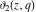 , , 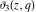 , and , and 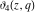 satisfy numerous relations that can provide transformations of their arguments, for example: satisfy numerous relations that can provide transformations of their arguments, for example:
Among those transformations, several kinds can be combined into specially named groups:
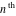 root of root of 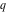 : :
Multiple angle formulas:
Double-angle formulas (which are not particular cases of the previous group), for example:
Landen's transformation:
Identities
The theta functions at 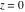 satisfy numerous modular identities of the form satisfy numerous modular identities of the form 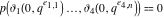 , where the , where the  are positive integers and are positive integers and 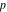 is a multivariate polynomials over the integers, for example: is a multivariate polynomials over the integers, for example:
Among the numerous identities for theta functions, several kinds can be joined into specially named groups:
Relations involving squares:
Relations involving quartic powers:
Relations between the four theta functions where the first argument is zero, for example:
Addition formulas:
Triple addition formulas, for example:
Representations of derivatives
The derivatives of the Jacobi theta functions 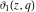 , , 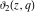 , , 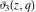 , and , and 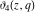 , and their derivatives , and their derivatives 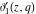 , , 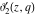 , , 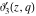 , and , and  with respect to variable with respect to variable 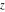 can be expressed by the following formulas: can be expressed by the following formulas:
The derivatives of the Jacobi theta functions 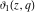 , , 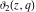 , , 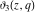 , and , and 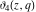 , and their derivatives , and their derivatives 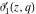 , , 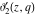 , , 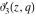 , and , and 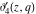 with respect to variable with respect to variable  can be expressed by the following formulas: can be expressed by the following formulas:
The 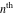 -order derivatives of the Jacobi theta functions -order derivatives of the Jacobi theta functions 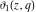 , ,  , , 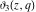 , and , and 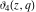 , and their derivatives , and their derivatives 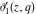 , , 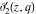 , , 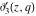 , and , and 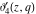 with respect to variable with respect to variable  can be expressed by the following formulas: can be expressed by the following formulas:
The 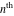 -order derivatives of Jacobi theta functions -order derivatives of Jacobi theta functions  , ,  , , 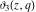 , and , and 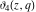 , and their derivatives , and their derivatives 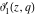 , , 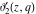 , , 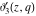 , and , and 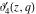 with respect to variable with respect to variable 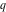 can be expressed by the following formulas: can be expressed by the following formulas:
Integration
The indefinite integrals of the Jacobi theta functions 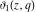 , , 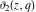 , , 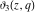 , and , and 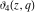 , and their derivatives , and their derivatives 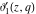 , , 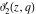 , , 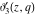 , and , and 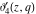 with respect to variable with respect to variable 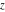 can be expressed by the following formulas: can be expressed by the following formulas:
The first four sums cannot be expressed in closed form through the named functions.
The indefinite integrals of the Jacobi theta functions 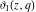 , ,  , , 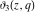 , and , and 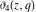 , and their derivatives , and their derivatives 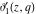 , , 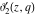 , , 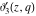 , and , and 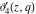 with respect to variable with respect to variable 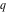 can be expressed by the following formulas: can be expressed by the following formulas:
Partial differential equations
The elliptic theta functions 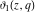 , , 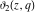 , , 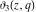 , and , and 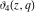 , and their derivatives , and their derivatives 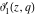 , , 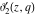 , ,  , and , and 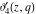 satisfy the one‐dimensional heat equations: satisfy the one‐dimensional heat equations:
The elliptic theta functions  , , 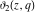 , ,  , and , and 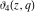 , and their derivatives , and their derivatives 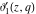 , ,  , , 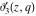 , and , and 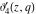 satisfy the following second-order partial differential equations: satisfy the following second-order partial differential equations:
Zeros
The Jacobi theta functions 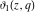 , ,  , , 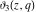 , and , and  , and their derivatives , and their derivatives 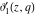 , , 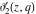 , , 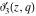 , and , and 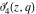 are equal to zero in the following points: are equal to zero in the following points:
Applications of Jacobi theta functions
Applications of the Jacobi theta functions include the analytic solution of the heat equation, square potential well problems in quantum mechanics, Wannier functions in solid state physics, conformal mapping of periodic regions, gravitational physics, quantum cosmology, coding theory, sphere packings, crystal lattice calculations, and study of the fractional quantum Hall effect.
|