|
General
The basic achievements in studying infinite series were made in the 18th and 19th centuries when mathematicians investigated issues regarding the convergence of different types of series. In particular, they found that the famous geometrical series:
converges inside the unit circle z < 1 to the function 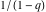 , but can be analytically extended outside this circle by the formulas , but can be analytically extended outside this circle by the formulas  and and 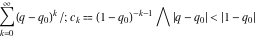 . The sums of these two series produce the same function . The sums of these two series produce the same function 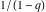 . But restrictions on convergence for all three series strongly depend on the distance between the center of expansion . But restrictions on convergence for all three series strongly depend on the distance between the center of expansion 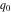 and the nearest singular point 1 (where the function and the nearest singular point 1 (where the function 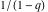 has a first-order pole). has a first-order pole).
The properties of the series:
lead to similar results, which attracted the interest of J. Bernoulli (1713), L. Euler, J. Fourier, and other researchers. They found that this series cannot be analytically continued outside the unit circle z < 1 because its boundary z ⩵ 1 has not one, but an infinite set of dense singular points. This boundary was called the natural boundary of analyticity of the corresponding function, which is defined as the sum of the previous series.
Special contributions to the theoretical development of these series were made by C. G. J. Jacobi (1827), who introduced the elliptic amplitude  and studied the twelve elliptic functions and studied the twelve elliptic functions  , ,  , , 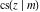 , , 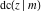 , , 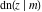 , , 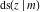 , , 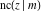 , , 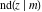 , ,  , , 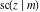 , ,  , , 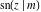 . All these functions later were named for Jacobi. C. G. J. Jacobi also introduced four basic theta functions, which can be expressed through the following series: . All these functions later were named for Jacobi. C. G. J. Jacobi also introduced four basic theta functions, which can be expressed through the following series:
These Jacobi elliptic theta functions notated by the symbols 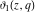 , , 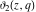 , ,  , and , and 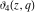 have the following representations: have the following representations:
A more detailed theory of elliptic theta functions was developed by C. W. Borchardt (1838), K. Weierstrass (1862–1863), and others. Many relations in the theory of elliptic functions include derivatives of the theta functions with respect to the variable 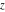 : : 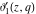 , , 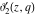 , ,  , and , and 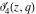 , which cannot be expressed through other special functions. For this reason, Mathematica includes not only four well-known theta functions, but also their derivatives. , which cannot be expressed through other special functions. For this reason, Mathematica includes not only four well-known theta functions, but also their derivatives.
|