|
Connections within the group of Jacobi theta functions and with other function groups
Representations through related equivalent functions
The elliptic theta functions 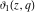 , , 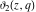 , , 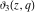 , and , and 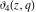 can be represented through the Weierstrass sigma functions by the following formulas: can be represented through the Weierstrass sigma functions by the following formulas:
where 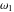 , , 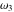 are the Weierstrass half-periods and are the Weierstrass half-periods and 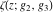 is the Weierstrass zeta function. is the Weierstrass zeta function.
The ratios of two different elliptic theta functions 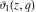 , , 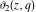 , , 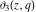 , and , and 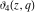 can be expressed through corresponding elliptic Jacobi functions with power factors by the following formulas: can be expressed through corresponding elliptic Jacobi functions with power factors by the following formulas:
where  is an elliptic nome and is an elliptic nome and 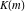 is a complete elliptic integral. is a complete elliptic integral.
Representations through other Jacobi theta functions
Each of the theta functions  , , 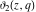 , , 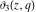 , and , and 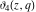 can be represented through the other theta functions by the following formulas: can be represented through the other theta functions by the following formulas:
The derivatives of the theta functions 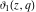 , , 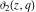 , , 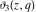 , and , and 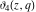 can also be expressed through the other theta functions and their derivatives by the following formulas: can also be expressed through the other theta functions and their derivatives by the following formulas:
|