|
General
Historical remarks
Jacobi functions are named for the famous mathematician C. G. J. Jacobi. In 1827 he introduced the elliptic amplitude 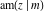 as the inverse function of the elliptic integral as the inverse function of the elliptic integral  by the variable by the variable  and investigated the twelve functions and investigated the twelve functions 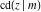 , , 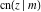 , , 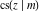 , , 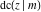 , , 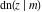 , , 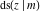 , , 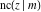 , , 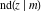 , ,  , ,  , , 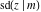 , and , and  . In the same year, N. H. Abel independently studied properties of these functions. But earlier K. F. Gauss (1799) gave some attention to one of these function, namely . In the same year, N. H. Abel independently studied properties of these functions. But earlier K. F. Gauss (1799) gave some attention to one of these function, namely  . .
The modern notations for Jacobi functions were introduced later in the works of C. Gudermann (1838) (for functions 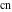 , , 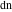 , and , and 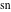 ) and J. Glaisher (1882) (for functions ) and J. Glaisher (1882) (for functions 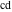 , , 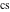 , , 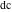 , , 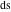 , ,  , , 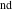 , , 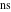 , , 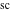 , and , and  ). V. A. Puiseux (1850) showed that amplitude ). V. A. Puiseux (1850) showed that amplitude  is a multivalued function. is a multivalued function.
Periodic functions
An analytic function  is called periodic if there exists a complex constant is called periodic if there exists a complex constant 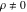 , such that , such that 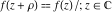 . The number . The number  (with minimal possible value of (with minimal possible value of 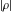 ) is called the period of the function ) is called the period of the function 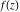 . .
Examples of well‐known singly periodic functions are the exponential functions and all the trigonometric and hyperbolic functions:  sin(z), cos(z), csc(z), sec(z), tan(z), cot(z), sinh(z), cosh(z), csch(z), sech(z), tanh(z), and coth(z), which have periods sin(z), cos(z), csc(z), sec(z), tan(z), cot(z), sinh(z), cosh(z), csch(z), sech(z), tanh(z), and coth(z), which have periods 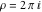 , , 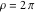 , , 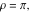  , and , and 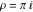 . The study of such functions can be restricted to any period‐strip . The study of such functions can be restricted to any period‐strip 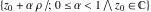 , because outside this strip, the values of these functions coincide with their corresponding values inside the strip. , because outside this strip, the values of these functions coincide with their corresponding values inside the strip.
Nonconstant analytic functions over the field of complex numbers cannot have more than two independent periods. So, generically, periodic functions can satisfy the following relations:
where 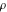 , ,  , and , and  are periods (basic primitive periods). The condition are periods (basic primitive periods). The condition 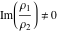 for doubly periodic functions implies the existence of a period‐parallelogram for doubly periodic functions implies the existence of a period‐parallelogram 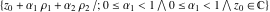 , which is the analog of the period‐strip , which is the analog of the period‐strip 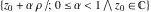 for the singly periodic function with period for the singly periodic function with period 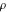 . .
In the case  this parallelogram is called the basic fundamental period‐parallelogram: this parallelogram is called the basic fundamental period‐parallelogram:  . The two line segments . The two line segments 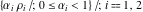 lying on the boundary of the period-parallelogram and beginning from the origin lying on the boundary of the period-parallelogram and beginning from the origin 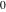 belong to belong to  . The region . The region  includes only one corner point includes only one corner point  from four points lying at the boundary of parallelogram with corners in from four points lying at the boundary of parallelogram with corners in 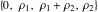 . Sometimes the convention . Sometimes the convention 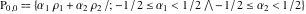 is used. is used.
The set of all such period‐parallelograms:
covers all complex planes: 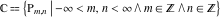 . .
Any doubly periodic function 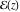 is called an elliptic function. The set of numbers is called an elliptic function. The set of numbers 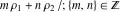 is called the period‐lattice for the elliptic function is called the period‐lattice for the elliptic function  . .
An elliptic function 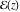 , which does not have poles in the period‐parallelogram, is equal to the constant Liouville's theorem. , which does not have poles in the period‐parallelogram, is equal to the constant Liouville's theorem.
Nonconstant elliptic (doubly periodic) functions 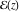 cannot be entire functions (this is not the case for singly periodic functions, for example, cannot be entire functions (this is not the case for singly periodic functions, for example, 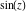 is an entire function. is an entire function.
Any nonconstant elliptic function 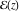 has at least two simple poles or at least one double pole in any period‐parallelogram. The sum of all its residues at the poles inside a period‐parallelogram is zero. has at least two simple poles or at least one double pole in any period‐parallelogram. The sum of all its residues at the poles inside a period‐parallelogram is zero.
The number of zeros and poles of a nonconstant elliptic function 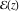 in a fundamental period‐parallelogram P are finite. in a fundamental period‐parallelogram P are finite.
The number of zeros of  , where , where  is any complex number, in a fundamental period‐parallelogram is any complex number, in a fundamental period‐parallelogram 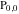 does not depend on the value does not depend on the value 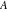 and coincides with the number and coincides with the number  of the poles of the poles 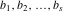 counted according to their multiplicity ( counted according to their multiplicity (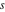 is called the order of the elliptic function is called the order of the elliptic function 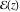 ). ).
The simplest elliptic function has order two.
Let 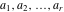 (and (and 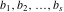 ) be the zeros (and poles) of a nonconstant elliptic function ) be the zeros (and poles) of a nonconstant elliptic function  in a fundamental period‐parallelogram in a fundamental period‐parallelogram 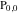 , both listed one or more times according to their multiplicity. This results in the following: , both listed one or more times according to their multiplicity. This results in the following:
So, the number of zeros of a nonconstant elliptic function 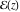 in the fundamental period‐parallelogram in the fundamental period‐parallelogram 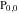 is equal to the number of poles there and counted according to their multiplicity. The sum of zeros of a nonconstant elliptic function is equal to the number of poles there and counted according to their multiplicity. The sum of zeros of a nonconstant elliptic function 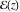 in the fundamental period‐parallelogram in the fundamental period‐parallelogram  differs from the sum of its poles by a period differs from the sum of its poles by a period 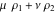 , where , where  and the values of and the values of  , , 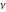 depend on the function depend on the function  . .
All elliptic functions 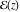 satisfy a common fundamental property, which generalizes addition, duplication, and multiple angle properties for the trigonometric and hyperbolic functions such as satisfy a common fundamental property, which generalizes addition, duplication, and multiple angle properties for the trigonometric and hyperbolic functions such as 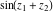 , , 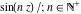 . It can be formulated as: . It can be formulated as:
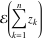 , ,
which can be expressed as an algebraic function of  . In other words, there exists an irreducible polynomial . In other words, there exists an irreducible polynomial 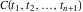 in in 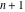 variables with constant coefficients, for which the following relation holds: variables with constant coefficients, for which the following relation holds:
Conversely, among all smooth functions, only elliptic functions and their degenerations have algebraic addition theorems.
The simplest elliptic functions (of order two) can be divide into the following two classes:
(1) Functions that at the period‐parallelogram 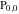 have only a double pole with a residue zero (e.g., the Weierstrass elliptic functions have only a double pole with a residue zero (e.g., the Weierstrass elliptic functions 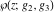 ). ).
(2) Functions that at the period‐parallelogram 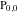 have only two simple poles with residues, which are equal in absolute value but opposite in sign (e.g., the Jacobian elliptic functions have only two simple poles with residues, which are equal in absolute value but opposite in sign (e.g., the Jacobian elliptic functions 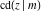 , , 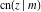 , , 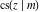 , , 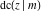 , , 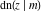 , , 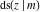 , , 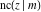 , , 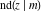 , , 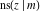 , , 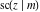 , , 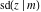 , and , and 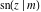 ). ).
Jacobian elliptic functions 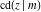 , , 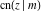 , , 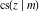 , , 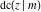 , , 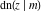 , , 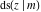 , , 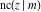 , , 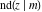 , ,  , , 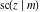 , , 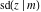 , and , and  arise as solutions to the differential equation: arise as solutions to the differential equation:
with the following coefficients:
|