|
The best-known properties and formulas for Jacobi functions
Real values for real arguments
For real values of arguments 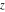 and and 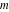 , the values of all Jacobi functions , the values of all Jacobi functions 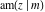 , , 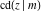 , ,  , ,  , , 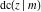 , ,  , , 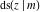 , , 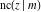 , , 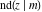 , , 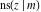 , , 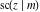 , , 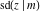 , and , and 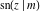 are real (or infinity). are real (or infinity).
Simple values at zero
All thirteen Jacobi functions  , , 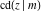 , , 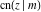 , ,  , , 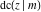 , , 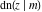 , , 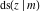 , ,  , , 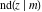 , , 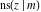 , , 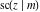 , , 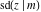 , and , and 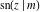 have the following simple values at the origin: have the following simple values at the origin:
Specific values for specialized parameter values
All Jacobi functions 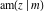 , , 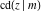 , ,  , , 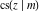 , , 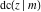 , , 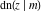 , , 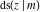 , ,  , ,  , , 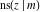 , , 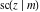 , , 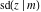 , and , and 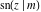 can be represented through elementary functions when can be represented through elementary functions when 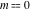 or or 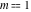 . The twelve elliptic functions degenerate into trigonometric and hyperbolic functions: . The twelve elliptic functions degenerate into trigonometric and hyperbolic functions:
All Jacobi functions 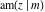 , , 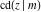 , , 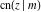 , , 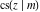 , ,  , , 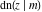 , ,  , , 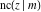 , , 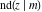 , , 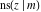 , , 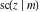 , , 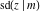 , and , and 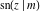 have very simple values at have very simple values at 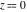 : :
The twelve Jacobi functions  , , 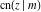 , , 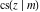 , , 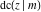 , , 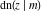 , , 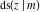 , , 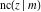 , , 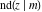 , , 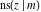 , , 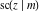 , , 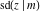 , and , and 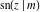 have the following values at the half‐quarter‐period points: have the following values at the half‐quarter‐period points:
The partial derivatives of all Jacobi functions 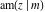 , , 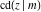 , , 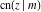 , , 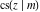 , , 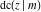 , , 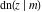 , , 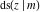 , ,  , , 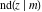 , , 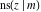 , , 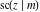 , ,  , and , and  at the points at the points 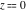 , , 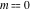 , or , or 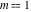 can be represented through trigonometric functions, for example: can be represented through trigonometric functions, for example:
Analyticity
All Jacobi functions 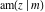 , , 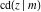 , , 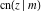 , ,  , , 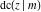 , , 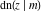 , , 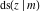 , , 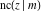 , ,  , , 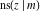 , , 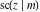 , , 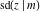 , and , and 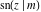 are analytical meromorphic functions of are analytical meromorphic functions of  and and  that are defined over that are defined over 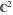 . .
Poles and essential singularities
The amplitude function 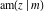 does not have poles and essential singularities with respect to does not have poles and essential singularities with respect to 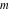 and and 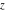 . .
For fixed 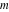 , all Jacobi functions , all Jacobi functions  , , 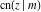 , , 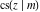 , , 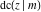 , , 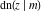 , , 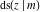 , , 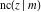 , , 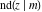 , , 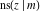 , , 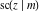 , , 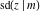 , and , and  have an infinite set of singular points, including simple poles in finite points and an essential singular point have an infinite set of singular points, including simple poles in finite points and an essential singular point  . .
The following formulas describe the sets of the simple poles for the corresponding Jacobi functions:
The values of the residues of the Jacobi functions at the simple poles are given by the following formulas:
Branch points and branch cuts
For fixed  , all Jacobi functions , all Jacobi functions  , , 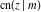 , , 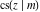 , ,  , , 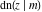 , ,  , , 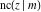 , , 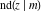 , , 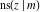 , , 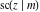 , , 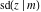 , and , and 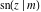 are meromorphic functions in are meromorphic functions in 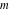 that have no branch points and branch cuts. that have no branch points and branch cuts.
For fixed  , all Jacobi functions , all Jacobi functions 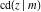 , ,  , , 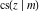 , , 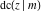 , , 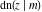 , , 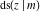 , , 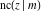 , , 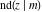 , ,  , ,  , , 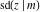 , and , and 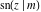 do not have branch points and branch cuts. do not have branch points and branch cuts.
Periodicity
The Jacobi amplitude 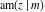 is a pseudo‐periodic function with respect to is a pseudo‐periodic function with respect to 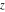 with period with period 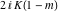 and pseudo‐period and pseudo‐period 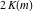 : :
The Jacobi functions 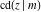 , , 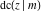 , , 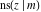 , and , and 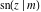 are doubly periodic functions with respect to are doubly periodic functions with respect to 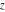 with periods with periods 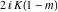 and and  . The Jacobi functions . The Jacobi functions 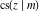 , ,  , ,  , and , and 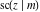 are doubly periodic functions with respect to are doubly periodic functions with respect to 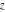 with periods with periods 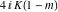 and and 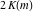 . The Jacobi functions . The Jacobi functions  , , 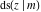 , , 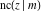 , and , and 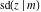 are doubly periodic functions with respect to are doubly periodic functions with respect to 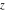 with periods with periods  and and 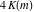 . That periodicity can be described by the following formulas: . That periodicity can be described by the following formulas:
The periodicity of Jacobi functions follow from more general formulas that also describe quasi‐periodicity situations such as  : :
Parity and symmetry
All Jacobi functions  , , 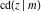 , , 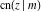 , , 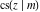 , ,  , , 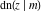 , ,  , , 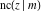 , , 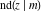 , , 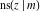 , , 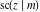 , ,  , and , and 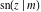 have mirror symmetry: have mirror symmetry:
The Jacobi functions 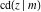 , , 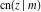 , ,  , , 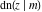 , , 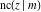 , and , and 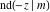 are even functions with respect to are even functions with respect to 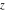 : :
The Jacobi functions 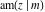 , ,  , , 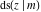 , , 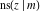 , , 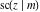 , , 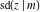 , and , and 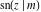 are odd functions with respect to are odd functions with respect to 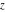 : :
Series representations
The Jacobi functions  , , 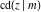 , , 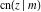 , , 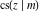 , , 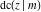 , , 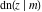 , , 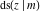 , , 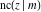 , ,  , , 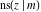 , , 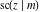 , , 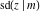 , and , and 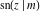 have the following series expansions at the point have the following series expansions at the point 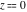 : :
The Jacobi functions  , , 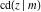 , , 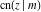 , , 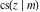 , ,  , , 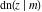 , , 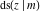 , ,  , , 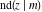 , , 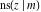 , , 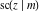 , , 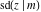 , and , and  have the following series expansions at the point have the following series expansions at the point 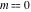 : :
The Jacobi functions 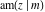 , , 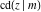 , , 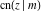 , , 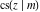 , , 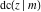 , , 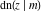 , , 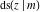 , , 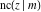 , , 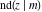 , ,  , , 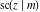 , , 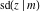 , and , and  have the following series expansions at the point have the following series expansions at the point 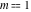 : :
q-series representations
The Jacobi functions 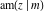 , , 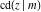 , , 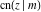 , , 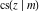 , , 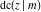 , , 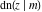 , , 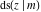 , , 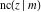 , , 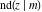 , , 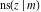 , ,  , , 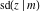 , and , and  have the following so-called q‐series representations: have the following so-called q‐series representations:
where 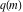 is the elliptic nome and is the elliptic nome and 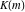 is the complete elliptic integral. is the complete elliptic integral.
Product representations
The twelve Jacobi functions 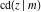 , , 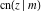 , , 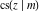 , , 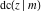 , , 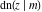 , , 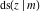 , , 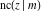 , , 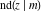 , , 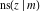 , , 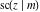 , , 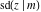 , and , and 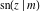 have the following product representations: have the following product representations:
where 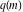 is the elliptic nome and is the elliptic nome and 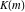 is the complete elliptic integral. is the complete elliptic integral.
Transformations
The amplitude function  satisfies numerous relations that allow for transformations of its arguments, for example: satisfies numerous relations that allow for transformations of its arguments, for example:
The twelve Jacobi functions  , , 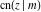 , , 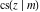 , ,  , , 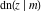 , , 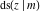 , ,  , , 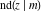 , ,  , , 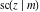 , , 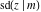 , and , and  with specific arguments can sometimes be represented through elliptic functions with other mostly simpler arguments, for example: with specific arguments can sometimes be represented through elliptic functions with other mostly simpler arguments, for example:
The twelve Jacobi functions 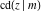 , , 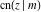 , , 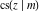 , , 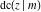 , , 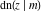 , , 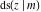 , , 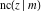 , , 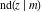 , ,  , , 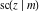 , , 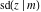 , and , and  with the argument complex with the argument complex 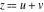 can be represented through elliptic functions with arguments can be represented through elliptic functions with arguments 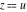 and and 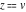 , for example: , for example:
The twelve Jacobi functions 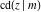 , , 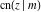 , , 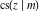 , , 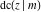 , , 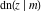 , , 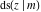 , ,  , , 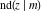 , , 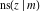 , , 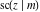 , , 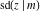 , and , and 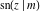 satisfy the following half‐angle formulas: satisfy the following half‐angle formulas:
The twelve Jacobi functions  , , 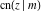 , ,  , , 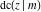 , , 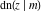 , , 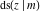 , , 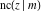 , , 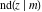 , , 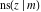 , , 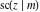 , , 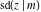 , and , and  satisfy the following double-angle (or multiplication) formulas: satisfy the following double-angle (or multiplication) formulas:
Identities
The twelve Jacobi functions 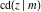 , ,  , , 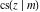 , , 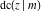 , , 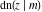 , , 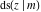 , ,  , , 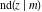 , ,  , , 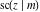 , , 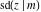 , and , and 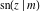 satisfy the following nonlinear functional equations: satisfy the following nonlinear functional equations:
Simple representations of derivatives
The derivatives of all Jacobi functions 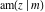 , , 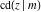 , , 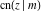 , , 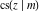 , , 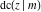 , , 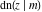 , , 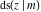 , , 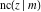 , , 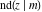 , , 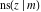 , , 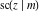 , , 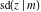 , and , and 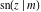 with respect to variable with respect to variable 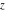 have rather simple and symmetrical representations that can be expressed through other Jacobi functions: have rather simple and symmetrical representations that can be expressed through other Jacobi functions:
The derivatives of all Jacobi functions 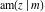 , , 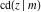 , , 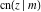 , , 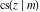 , , 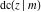 , , 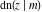 , , 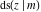 , , 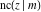 , ,  , , 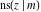 , , 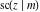 , ,  , and , and 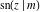 with respect to variable with respect to variable 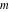 have more complicated representations that include other Jacobi functions and the elliptic integral have more complicated representations that include other Jacobi functions and the elliptic integral 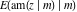 : :
Integration
The indefinite integrals of the twelve Jacobi functions 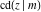 , , 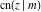 , , 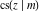 , ,  , , 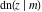 , , 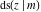 , ,  , , 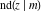 , , 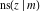 , , 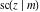 , , 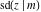 , and , and 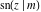 with respect to variable with respect to variable 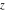 can be expressed through Jacobi and elementary functions by the following formulas: can be expressed through Jacobi and elementary functions by the following formulas:
Differential equations
The Jacobi amplitude 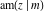 satisfies the following differential equations: satisfies the following differential equations:
All Jacobi functions 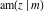 , , 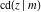 , , 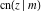 , , 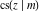 , , 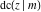 , , 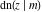 , , 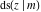 , ,  , , 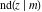 , , 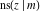 , , 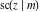 , , 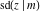 , and , and 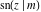 are special solutions of ordinary second-order nonlinear differential equations: are special solutions of ordinary second-order nonlinear differential equations:
The twelve Jacobi functions  , , 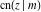 , , 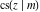 , , 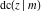 , ,  , , 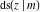 , ,  , , 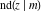 , , 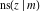 , , 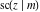 , , 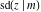 , and , and 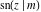 satisfy very complicated ordinary differential equations with respect to variable satisfy very complicated ordinary differential equations with respect to variable  , for example: , for example:
Zeros
All Jacobi functions 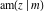 , , 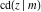 , , 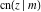 , , 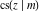 , ,  , , 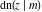 , , 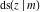 , , 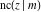 , , 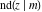 , , 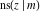 , ,  , , 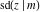 , and , and 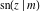 are equal to zero in the points are equal to zero in the points 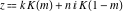 , where , where 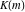 is the complete elliptic integral of the first kind and is the complete elliptic integral of the first kind and 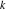 , , 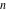 are even or odd integers: are even or odd integers:
|