|
The best-known properties and formulas for Weierstrass functions and inverses
Simple values at zero
The Weierstrass functions 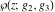 , , 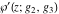 , , 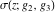 , and , and 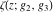 have the following simple values at the origin point: have the following simple values at the origin point:
Specific values for specialized parameter
The Weierstrass functions 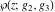 , , 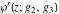 , , 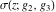 , , 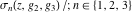 , and , and 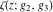 can be represented through elementary functions, when can be represented through elementary functions, when 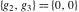 or or 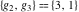 : :
At points 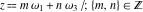 , all Weierstrass functions , all Weierstrass functions 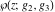 , , 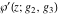 , , 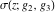 , , 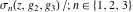 , and , and 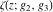 can be equal to zero or can have poles and be equal to can be equal to zero or can have poles and be equal to 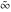 : :
The values of Weierstrass functions 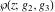 , , 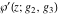 , , 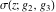 , , 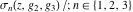 , and , and 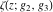 at the points at the points 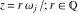 can sometimes be evaluated in closed form: can sometimes be evaluated in closed form:
The Weierstrass functions 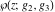 , , 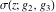 , and , and 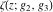 have rather simple values, when have rather simple values, when 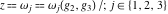 and and 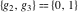 or or 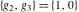 : :
The Weierstrass functions 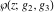 , , 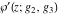 , , 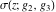 , and , and 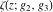 can be represented through elementary functions, when can be represented through elementary functions, when 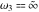 : :
Analyticity
The Weierstrass functions 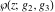 , , 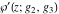 , , 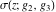 , , 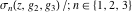 , , 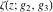 , and , and 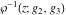 are analytical functions of are analytical functions of 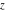 , , 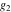 , and , and 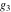 , which are defined in , which are defined in 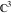 . The inverse Weierstrass function . The inverse Weierstrass function 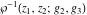 is an analytical function of is an analytical function of 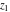 , , 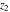 , , 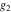 , , 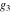 , which is also defined in , which is also defined in 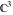 , because , because 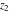 is not an independent variable. is not an independent variable.
Poles and essential singularities
For fixed 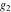 , , 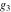 , the Weierstrass functions , the Weierstrass functions 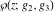 , , 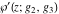 , and , and 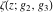 have an infinite set of singular points: have an infinite set of singular points:
(a) 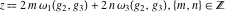 are the poles of order 2 with residues 0 (for are the poles of order 2 with residues 0 (for 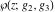 ), of order 3 with residues 0 (for ), of order 3 with residues 0 (for 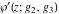 ) and simple poles with residues 1 (for ) and simple poles with residues 1 (for 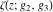 ). ).
(b) 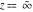 is an essential singular point. is an essential singular point.
For fixed 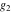 , , 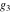 , the Weierstrass functions , the Weierstrass functions 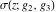 and and 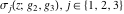 have only one singular point at have only one singular point at 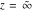 . It is an essential singular point. . It is an essential singular point.
The Weierstrass functions 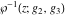 and and 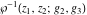 do not have poles and essential singularities with respect to their variables. do not have poles and essential singularities with respect to their variables.
Branch points and branch cuts
For fixed 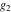 , , 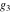 , the Weierstrass functions , the Weierstrass functions 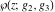 , , 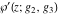 , , 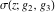 , , 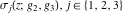 , and , and 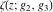 do not have branch points and branch cuts. do not have branch points and branch cuts.
For fixed 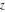 , , 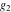 , the inverse Weierstrass function , the inverse Weierstrass function 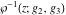 has two branch points: has two branch points: 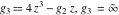 . .
For fixed 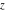 , , 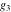 , the inverse Weierstrass function , the inverse Weierstrass function 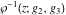 has two branch points: has two branch points: 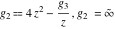 . .
For fixed 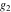 , , 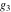 , the inverse Weierstrass function , the inverse Weierstrass function 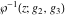 has four branch points: has four branch points: 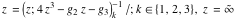 . .
Periodicity
The Weierstrass functions 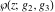 and and 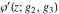 are doubly periodic functions with respect to are doubly periodic functions with respect to 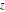 with periods with periods 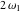 and and 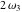 : :
The Weierstrass functions 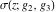 , , 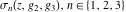 , and , and 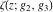 are quasi‐periodic functions with respect to are quasi‐periodic functions with respect to 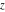 : :
The inverse Weierstrass functions 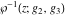 and and 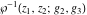 do not have periodicity and symmetry. do not have periodicity and symmetry.
Transformation of half-periods
The Weierstrass functions 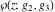 , , 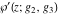 , , 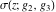 , , 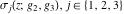 , and , and 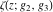 are the invariant functions under the linear transformation of the half‐periods are the invariant functions under the linear transformation of the half‐periods 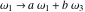 , , 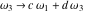 with integer coefficients with integer coefficients 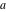 , , 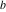 , , 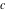 , and , and 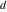 , satisfying restrictions , satisfying restrictions 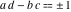 (modular transformations): (modular transformations):
Homogeneity
The Weierstrass functions 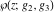 , , 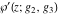 , , 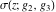 , , 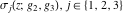 , and , and 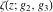 satisfy the following homogeneity type relations: satisfy the following homogeneity type relations:
Parity and symmetry
The Weierstrass functions 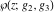 , , 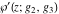 , , 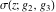 , , 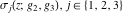 , , 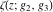 , and , and 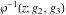 have mirror symmetry: have mirror symmetry:
The Weierstrass functions 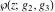 and and 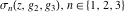 are even functions with respect to are even functions with respect to 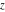 : :
The Weierstrass functions 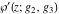 , , 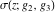 , and , and 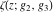 are odd functions with respect to are odd functions with respect to 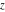 : :
Series representations
The Weierstrass functions 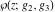 , , 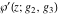 , , 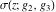 , and , and 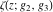 have the following series expansions at the point have the following series expansions at the point 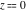 : :
The inverse Weierstrass function 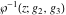 has the following series expansion at the point has the following series expansion at the point 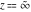 : :
q-series representations
The Weierstrass functions 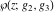 , , 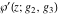 , , 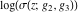 , , 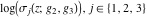 , and , and 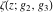 have the following so-called have the following so-called 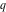 ‐series representations: ‐series representations:
Other series representations
The Weierstrass functions 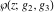 , , 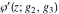 , , 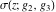 , , 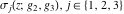 , and , and 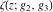 with with 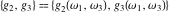 can be represented through series of different forms, for example: can be represented through series of different forms, for example:
Integral representations
The Weierstrass functions and their inverses 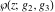 , , 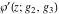 , , 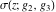 , , 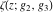 , , 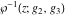 , and , and 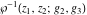 can be represented through the following integrals from elementary or Weierstrass functions: can be represented through the following integrals from elementary or Weierstrass functions:
Product representations
The Weierstrass functions 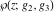 , , 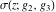 , and , and 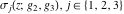 have the following product representations: have the following product representations:
q-product representations
The Weierstrass functions 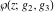 , , 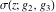 , and , and 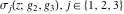 can be represented as so-called can be represented as so-called 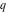 ‐products by the following formulas: ‐products by the following formulas:
Transformations
The Weierstrass functions 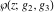 , , 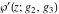 , , 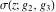 , , 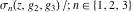 , and , and 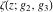 satisfy numerous relations that can provide transformations of its arguments. One of these transformations simplifies argument satisfy numerous relations that can provide transformations of its arguments. One of these transformations simplifies argument 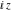 to to 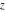 , for example: , for example:
Other transformations are described by so-called addition formulas:
Half‐angle formulas provide one more type of transformation, for example:
The Weierstrass functions 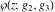 , , 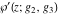 , , 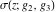 , and , and 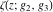 satisfy the following double-angle formulas: satisfy the following double-angle formulas:
These formulas can be expanded on triple angle formulas, for example:
Generally the following multiple angle formulas take place:
Sometimes transformations have a symmetrical character, which includes operations like determinate, for example:
A special class of transformation includes the simplification of Weierstrass functions 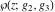 , , 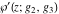 , , 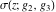 , , 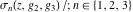 , and , and 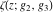 with invariants with invariants 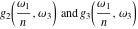 , where , where 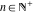 , for example: , for example:
Identities
The Weierstrass functions satisfy numerous functional identities, for example:
Representations of derivatives
The first two derivatives of all Weierstrass functions 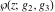 , , 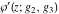 , , 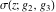 , , 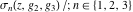 , and , and 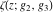 , and their inverses , and their inverses 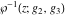 and and 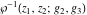 with respect to variable with respect to variable 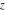 can also be expressed through Weierstrass functions: can also be expressed through Weierstrass functions:
The first derivatives of Weierstrass functions 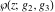 , , 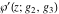 , , 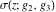 , and , and 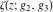 with respect to parameter with respect to parameter 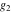 can also be expressed through Weierstrass functions by the following formulas: can also be expressed through Weierstrass functions by the following formulas:
The first derivatives of Weierstrass functions 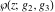 , , 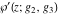 , , 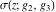 , and , and 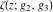 with respect to parameter with respect to parameter 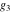 can also be expressed through Weierstrass functions by the following formulas: can also be expressed through Weierstrass functions by the following formulas:
Weierstrass invariants 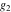 and and 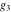 can be expressed as functions of half-periods can be expressed as functions of half-periods 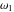 and and 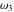 . This property allows obtaining the following formulas for the first derivatives of Weierstrass functions . This property allows obtaining the following formulas for the first derivatives of Weierstrass functions 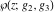 , , 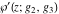 , , 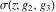 , and , and 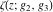 with respect to half-period with respect to half-period 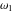 : :
Similar formulas take place for the first derivatives of Weierstrass functions 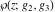 , , 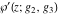 , , 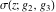 , and , and 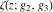 with respect to half-period with respect to half-period 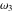 : :
The 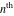 derivatives of all Weierstrass functions derivatives of all Weierstrass functions 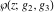 , , 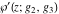 , , 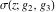 , , 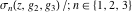 , , 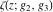 , and their inverses , and their inverses 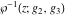 and and 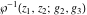 with respect to variable with respect to variable 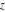 can be represented by the following formulas: can be represented by the following formulas:
Integration
The indefinite integrals of Weierstrass functions 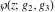 , , 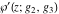 , , 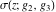 , and , and 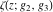 with respect to variable with respect to variable 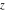 can be expressed by the following formulas: can be expressed by the following formulas:
Summation
Finite and infinite sums including Weierstrass functions can sometimes be evaluated in closed forms, for example:
Differential equations
The Weierstrass functions 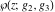 , , 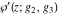 , , 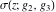 , , 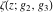 , and their inverses , and their inverses 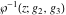 and and 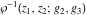 satisfy the following nonlinear differential equations: satisfy the following nonlinear differential equations:
The Weierstrass functions 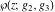 , , 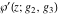 , , 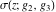 , and , and 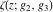 are the special solutions of the corresponding partial differential equations: are the special solutions of the corresponding partial differential equations:
|