|
Introduction to the Weierstrass utility functions
General
The creation and development of the elliptic functions' theory in the 18th century required the introduction of special supporting utility functions, which were frequently used for description of the properties of the elliptic functions. Among such utilities the basic role is played by so-called Weierstrass invariants and Weierstrass half-periods. These were given the unusual notations 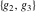 and { and {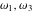 } instead of a consecutive numbering. The Weierstrass utility functions are a pair of bivariate functions that are inverses of each other: } instead of a consecutive numbering. The Weierstrass utility functions are a pair of bivariate functions that are inverses of each other:
Half-periods 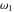 and and 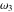 (and (and 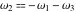 ) were mentioned in the works of C. G. J. Jacobi (1835), K. Weierstrass (1862), and A. Hurwitz (1905). The invariants ) were mentioned in the works of C. G. J. Jacobi (1835), K. Weierstrass (1862), and A. Hurwitz (1905). The invariants 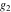 and and 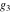 were mentioned in the works of A. Cayley and G. Boole (1845). were mentioned in the works of A. Cayley and G. Boole (1845).
Numerous formulas of Weierstrass elliptic functions include values of the Weierstrass 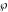 function and the Weierstrass zeta functions function and the Weierstrass zeta functions 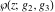 and and 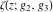 at the points at the points 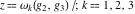 . These values have the following widely used notations: . These values have the following widely used notations:
Definitions of Weierstrass utilities
The Weierstrass half‐periods 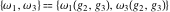 and the Weierstrass invariants and the Weierstrass invariants 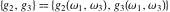 , the Weierstrass , the Weierstrass  function values at half-periods function values at half-periods 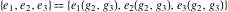 , and the Weierstrass zeta function values at half-periods , and the Weierstrass zeta function values at half-periods 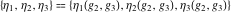 are defined by the following formulas: are defined by the following formulas:
where 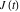 is the Klein invariant modular function, is the Klein invariant modular function, 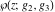 is Weierstrass elliptic is Weierstrass elliptic 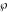 function, and function, and 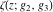 is theWeierstrass zeta function. is theWeierstrass zeta function.
The previous four vector functions are sometimes called the Weierstrass utilities because they are the basic elements of the Weierstrass theory of elliptic functions.
A quick look at the Weierstrass utilities The following graphics show the values of the real and imaginary parts of the Weierstrass half-periods over the real 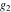 ‐ ‐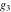 plane. plane. The following graphics show the values of the real and imaginary parts of the Weierstrass invarants over the 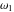 ‐ ‐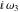 plane. plane. The following graphics show the values of the real and imaginary parts of the Weierstrass 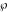 function at the half-periods over the real function at the half-periods over the real 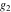 ‐ ‐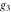 plane. plane. The following graphics show the values of the real and imaginary parts of the Weierstrass zeta function at the half-periods over the real 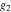 ‐ ‐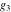 plane. plane.
Connections within the group of Weierstrass utilities and inverses and with other function groups
Representations through related equivalent functions
The Weierstrass half‐periods 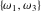 can be represented through the complete elliptic integral can be represented through the complete elliptic integral 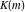 and the inverse elliptic nome and the inverse elliptic nome 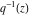 by the formula: by the formula:
The Weierstrass invariants 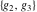 can be represented through the complete elliptic integral can be represented through the complete elliptic integral 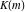 , the inverse elliptic nome , the inverse elliptic nome 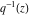 , the modular lambda function , the modular lambda function 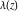 , and the theta functions , and the theta functions 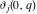 by the following formulas: by the following formulas:
The Weierstrass 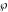 function values function values  at half-periods can be represented through the complete elliptic integral at half-periods can be represented through the complete elliptic integral 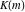 , the modular lambda function , the modular lambda function 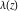 , the Weierstrass sigma function , the Weierstrass sigma function 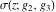 , and the theta functions , and the theta functions 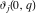 by the following formulas: by the following formulas:
The Weierstrass zeta function values at half-periods 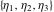 can be represented through the complete elliptic integrals can be represented through the complete elliptic integrals 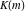 and and 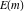 , the modular lambda function , the modular lambda function 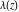 , and the theta functions , and the theta functions 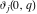 by the following formulas: by the following formulas:
Relations to inverse functions
The following formula shows that the Weierstrass half‐periods 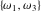 play the role of inverse functions to the Weierstrass invariants play the role of inverse functions to the Weierstrass invariants 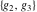 : :
Representations through other Weierstrass utilities
The Weierstrass half‐periods 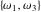 , the invariants , the invariants 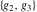 , and the Weierstrass , and the Weierstrass 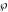 function values at half-periods function values at half-periods 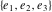 are connected by the following formulas: are connected by the following formulas:
The best-known properties and formulas for Weierstrass utilities
Specific values
The Weierstrass invariants 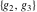 have the following values at infinities: have the following values at infinities:
The Weierstrass 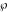 function values at half-periods function values at half-periods 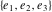 can be evaluated at closed forms for some values of arguments can be evaluated at closed forms for some values of arguments 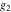 , , 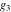 : :
The Weierstrass zeta function values at half-periods 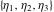 can also be evaluated at closed forms for some values of arguments can also be evaluated at closed forms for some values of arguments 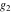 , , 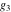 : :
Analyticity
The Weierstrass half‐periods 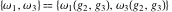 , the Weierstrass , the Weierstrass 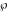 function values at half-periods function values at half-periods 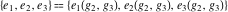 , and the Weierstrass zeta function values at half-periods , and the Weierstrass zeta function values at half-periods 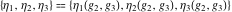 are vector‐valued functions of are vector‐valued functions of 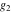 and and  that are analytic in each vector component, and they are defined over that are analytic in each vector component, and they are defined over 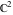 . .
The Weierstrass invariants 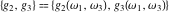 is a vector‐valued function of is a vector‐valued function of 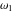 and and 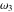 that is analytic in each vector component, and it is defined over that is analytic in each vector component, and it is defined over 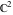 (for (for 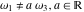 ). ).
Periodicity
The Weierstrass invariants 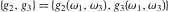 with with 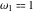 is a periodic function with period is a periodic function with period 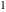 : :
The other Weierstrass utility functions 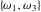 , , 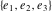 , and , and 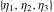 are not periodic functions. are not periodic functions.
Parity and symmetry
The Weierstrass half‐periods 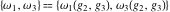 and Weierstrass zeta function values at half-periods and Weierstrass zeta function values at half-periods 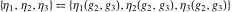 have mirror symmetry: have mirror symmetry:
The Weierstrass invariants 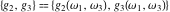 and the Weierstrass and the Weierstrass 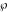 function values at half-periods function values at half-periods 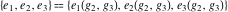 have standard mirror symmetry: have standard mirror symmetry:
The Weierstrass invariants  have permutation symmetry and are homogeneous: have permutation symmetry and are homogeneous:
The Weierstrass invariants 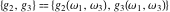 are the invariants under the change of variables are the invariants under the change of variables 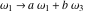 and and 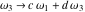 with integers with integers 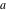 , , 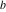 , , 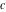 , and , and 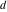 , satisfying the restriction , satisfying the restriction 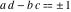 (modular transformations): (modular transformations):
This property leads to similar properties of the Weierstrass 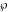 function values at half-periods function values at half-periods 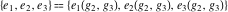 and the Weierstrass zeta function values at half-periods and the Weierstrass zeta function values at half-periods 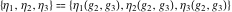 : :
Series representations
The Weierstrass half‐periods 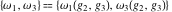 and invariants and invariants 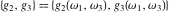 have the following double series expansions: have the following double series expansions:
where 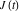 is a Klein invariant modular function. is a Klein invariant modular function.
The last double series can be rewritten in the following forms:
q-series representations
The Weierstrass invariants 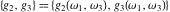 , the Weierstrass , the Weierstrass 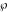 function values at half-periods function values at half-periods 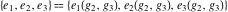 , and the Weierstrass zeta function values at half-periods , and the Weierstrass zeta function values at half-periods 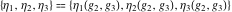 have numerous q‐series representations, for example: have numerous q‐series representations, for example:
where 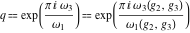 . .
The following rational function of 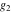 and and 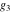 is a modular function if considered as a function of is a modular function if considered as a function of 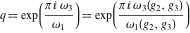 : :
Other series representations
The Weierstrass utilities have some other forms of series expansions, for example:
where 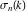 is the divisor sigma function. is the divisor sigma function.
Integral representations
The Weierstrass half‐periods 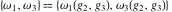 and invariants and invariants 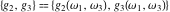 have the following integral representations: have the following integral representations:
Product representations
The Weierstrass utilities can have product representations. For example, the Weierstrass 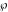 function values at half-periods function values at half-periods 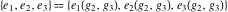 can be expressed through the following products: can be expressed through the following products:
where 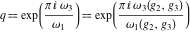 . .
Identities
The Weierstrass utilities satisfy numerous identities, for example:
Representations of derivatives
The first derivatives of Weierstrass half‐periods 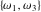 and the Weierstrass and the Weierstrass 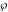 and zeta function values at half-periods and zeta function values at half-periods 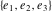 and and 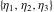 with respect to variable with respect to variable 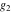 and and 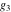 have the following representations: have the following representations:
where 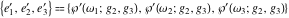 are the values of the derivative of the Weierstrass elliptic are the values of the derivative of the Weierstrass elliptic 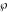 function function 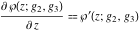 at half-period points at half-period points 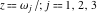 . .
The first derivatives of Weierstrass invariants 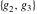 with respect to the variables with respect to the variables 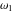 and and 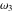 can be represented in different forms: can be represented in different forms:
The 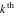 -order derivatives of Weierstrass invariants -order derivatives of Weierstrass invariants 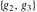 with respect to the variables with respect to the variables 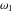 and and 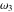 have the following representations: have the following representations:
Integration
The indefinite integrals of Weierstrass invariants 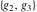 with respect to the variable with respect to the variable 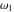 have the following representations: have the following representations:
Differential equations
The Weierstrass half‐periods 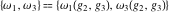 satisfy the following differential equations: satisfy the following differential equations:
The Weierstrass invariants 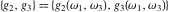 satisfy the following differential equations: satisfy the following differential equations:
The Weierstrass zeta function values at half-periods 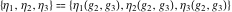 satisfy the following differential equations: satisfy the following differential equations:
Applications of Weierstrass utilities
Applications of Weierstrass utilities include the application areas of the Weierstrass elliptic functions, such as integrable nonlinear differential equations, motion in cubic and quartic potentials, description of the movement of a spherical pendulum, and construction of minimal surfaces.
|