|
The Weierstrass half‐periods  can be represented through the complete elliptic integral can be represented through the complete elliptic integral 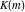 and the inverse elliptic nome and the inverse elliptic nome 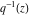 by the formula: by the formula:
The Weierstrass invariants 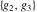 can be represented through the complete elliptic integral can be represented through the complete elliptic integral 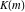 , the inverse elliptic nome , the inverse elliptic nome 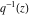 , the modular lambda function , the modular lambda function 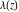 , and the theta functions , and the theta functions  by the following formulas: by the following formulas:
The Weierstrass 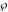 function values function values 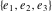 at half-periods can be represented through the complete elliptic integral at half-periods can be represented through the complete elliptic integral 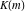 , the modular lambda function , the modular lambda function 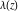 , the Weierstrass sigma function , the Weierstrass sigma function 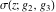 , and the theta functions , and the theta functions 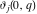 by the following formulas: by the following formulas:
The Weierstrass zeta function values at half-periods 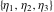 can be represented through the complete elliptic integrals can be represented through the complete elliptic integrals 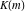 and and  , the modular lambda function , the modular lambda function 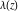 , and the theta functions , and the theta functions 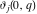 by the following formulas: by the following formulas:
The following formula shows that the Weierstrass half‐periods 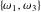 play the role of inverse functions to the Weierstrass invariants play the role of inverse functions to the Weierstrass invariants  : :
The Weierstrass half‐periods 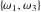 , the invariants , the invariants 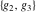 , and the Weierstrass , and the Weierstrass  function values at half-periods function values at half-periods 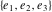 are connected by the following formulas: are connected by the following formulas:
|