|
The best-known properties and formulas for complete elliptic integrals
Real values for real restricted arguments
For real values of arguments 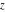 , , 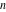 , and , and 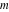 (with (with 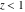 , , 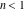 , , 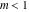 ) the values of all complete elliptic integrals ) the values of all complete elliptic integrals 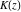 , , 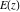 , and , and 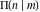 are real. are real.
Simple values at zero
All complete elliptic integrals 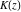 , ,  , and , and 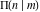 are equal to are equal to 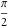 at the origin: at the origin:
Specific values
All complete elliptic integrals 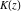 , , 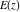 , and , and 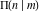 can be represented through elementary or other functions when can be represented through elementary or other functions when  , , 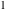 , or , or 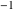 , , 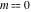 or or 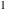 , or , or 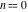 or or 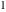 : :
At any infinity, the complete elliptic integrals 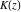 , , 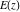 , and , and 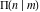 have the following values: have the following values:
Analyticity
The complete elliptic integrals  and and 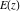 are analytical functions of are analytical functions of 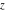 , which are defined over the whole complex , which are defined over the whole complex 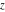 ‐plane. ‐plane.
The complete elliptic integral 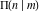 is an analytical function of is an analytical function of 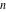 and and 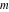 , which is defined over , which is defined over 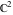 . .
Poles and essential singularities
All complete elliptic integrals 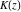 , , 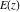 , and , and  do not have poles and essential singularities. do not have poles and essential singularities.
Branch points and branch cuts
The complete elliptic integrals  and and 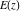 have two branch points: have two branch points: 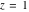 and and 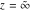 . .
They are single‐valued functions on the 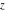 ‐plane cut along the interval ‐plane cut along the interval 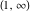 . They are continuous from below on the interval . They are continuous from below on the interval 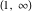 : :
For fixed  , the function , the function 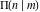 has two branch points at has two branch points at 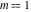 and and 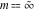 . For fixed . For fixed 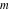 , the function , the function  has two branch points at has two branch points at 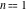 and and 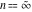 . .
Periodicity
All complete elliptic integrals 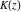 , , 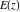 , and , and 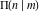 are not periodical functions. are not periodical functions.
Parity and symmetry
All complete elliptic integrals  , , 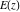 , and , and 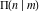 have mirror symmetry: have mirror symmetry:
Series representations
All complete elliptic integrals  , , 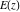 , and , and 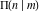 have the following series expansions at the point have the following series expansions at the point 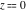 : :
The complete elliptic integrals 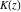 and and 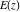 have the following series expansions at the point have the following series expansions at the point 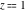 : :
The complete elliptic integrals 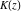 and and 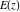 have the following series expansions at the point have the following series expansions at the point 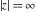 : :
The complete elliptic integral  has the following series expansions at the point has the following series expansions at the point 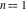 : :
The complete elliptic integral 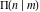 has the following series expansions at the point has the following series expansions at the point  : :
The complete elliptic integral 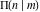 has the following series expansions at the point has the following series expansions at the point 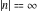 : :
The complete elliptic integral 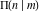 has the following series expansions at the point has the following series expansions at the point  : :
The previous formulas can be rewritten in summed forms of the truncated series expansion near corresponding points  , , 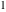 , or , or 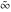 : :
Other series representations
Some elliptic integrals have special series representations through the elliptic nome  and inverse Jacobi elliptic functions by the formulas: and inverse Jacobi elliptic functions by the formulas:
Integral representations
The complete elliptic integrals  , , 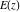 , and , and  have the following integral representations: have the following integral representations:
Identities
The complete elliptic integrals 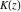 , ,  , and , and 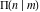 satisfy numerous identities, for example: satisfy numerous identities, for example:
Representations of derivatives
The first derivatives of all complete elliptic integrals 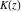 , , 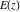 , and , and 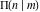 with respect to their variables can also be represented through complete elliptic integrals by the following formulas: with respect to their variables can also be represented through complete elliptic integrals by the following formulas:
The symbolic 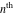 derivatives of all complete elliptic integrals derivatives of all complete elliptic integrals  , , 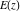 , and , and 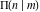 with respect to their variables can be represented through Gauss classical or regularized hypergeometric functions by the following formulas: with respect to their variables can be represented through Gauss classical or regularized hypergeometric functions by the following formulas:
Integration
The indefinite integrals of all complete elliptic integrals 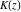 , , 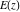 , and , and 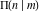 with respect to their variables can be expressed through complete elliptic integrals (or through hypergeometric functions of two variables) by the following formulas: with respect to their variables can be expressed through complete elliptic integrals (or through hypergeometric functions of two variables) by the following formulas:
Differential equations
All complete elliptic integrals 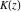 , ,  , and , and 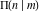 satisfy ordinary linear differential equations: satisfy ordinary linear differential equations:
|