|
Introduction to the complete elliptic integrals
General
Elliptic integrals were introduced in the investigations of J. Wallis (1655–1659) who studied the integral (in modern notation):
L. Euler (1733, 1757, 1763, 1766) derived the addition theorem for the following elliptic integrals currently called incomplete elliptic integrals of the first and second kind:
J.‐L. Lagrange (1783) and especially A. M. Legendre (1793, 1811, 1825–1828) devoted considerable attention to study different properties of these integrals. C. F. Gauss (1799, 1818) also used these integrals during his research.
Simultaneously, A. M. Legendre (1811) introduced the incomplete elliptic integral of the third kind:
and the complete versions of the integrals:
C. G. J. Jacobi (1827–1829) introduced inverse functons of the elliptic integrals 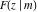 and and 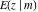 , which lead him to build the theory of elliptic functions. In 1829 C. G. J. Jacobi defined the function: , which lead him to build the theory of elliptic functions. In 1829 C. G. J. Jacobi defined the function:
which was later called the Jacobi zeta function. J. Liouville (1840) also studied the elliptic integrals 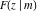 and and 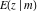 . .
N. H. Abel independently derived some of C. G. J. Jacobi's results and studied the so-called hyperelliptic and Abelian integrals.
Definitions of complete elliptic integrals
The complete elliptic integral of the first kind  , the complete elliptic integral of the second kind , the complete elliptic integral of the second kind 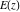 , and the complete elliptic integral of the third kind , and the complete elliptic integral of the third kind 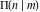 are defined through the following formulas: are defined through the following formulas:
where the incomplete elliptic integrals of the first, second, and third kind are as follows:
A quick look at the complete elliptic integrals Here is a quick look at the graphics for the complete elliptic integrals along the real axis.
Connections within the group of complete elliptic integrals and with other function groups
Representations through more general functions
All complete elliptic integrals 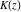 , , 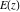 , and , and 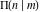 can be represented through more general functions.
Through the Gauss hypergeometric function: can be represented through more general functions.
Through the Gauss hypergeometric function:
Through the Meijer G function:
Through the hypergeometric Appell  function of two variables: function of two variables:
Through the hypergeometric function of two variables:
Through the incomplete elliptic integrals:
Through the elliptic theta functions:
Through the arithmetic geometric mean:
Through the Jacobi elliptic functions:
Through the Weierstrass elliptic functions and inverse elliptic nome 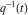 : :
Through the Legendre 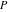 and and 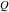 functions: functions:
Relations to inverse functions
The complete elliptic integral 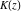 is related to Jacobi amplitude by the following formula, which demonstrates that Jacobi amplitude is the some kind of inverse function to the elliptic integral is related to Jacobi amplitude by the following formula, which demonstrates that Jacobi amplitude is the some kind of inverse function to the elliptic integral 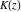 : :
Representations through other complete elliptic integrals
All complete elliptic integrals  , , 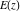 , and , and 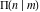 can be represented through other complete elliptic integrals by the following formulas: can be represented through other complete elliptic integrals by the following formulas:
The best-known properties and formulas for complete elliptic integrals
Real values for real restricted arguments
For real values of arguments 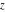 , , 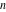 , and , and 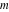 (with (with 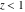 , , 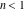 , , 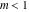 ) the values of all complete elliptic integrals ) the values of all complete elliptic integrals 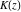 , , 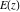 , and , and 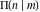 are real. are real.
Simple values at zero
All complete elliptic integrals 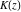 , ,  , and , and 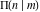 are equal to are equal to 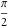 at the origin: at the origin:
Specific values
All complete elliptic integrals 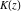 , , 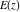 , and , and 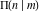 can be represented through elementary or other functions when can be represented through elementary or other functions when  , ,  , or , or 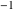 , , 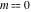 or or 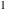 , or , or 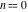 or or 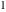 : :
At any infinity, the complete elliptic integrals 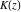 , , 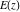 , and , and 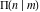 have the following values: have the following values:
Analyticity
The complete elliptic integrals  and and 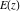 are analytical functions of are analytical functions of 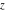 , which are defined over the whole complex , which are defined over the whole complex 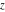 ‐plane. ‐plane.
The complete elliptic integral 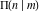 is an analytical function of is an analytical function of 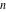 and and 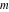 , which is defined over , which is defined over 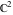 . .
Poles and essential singularities
All complete elliptic integrals 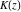 , , 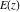 , and , and  do not have poles and essential singularities. do not have poles and essential singularities.
Branch points and branch cuts
The complete elliptic integrals  and and 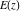 have two branch points: have two branch points: 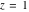 and and 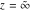 . .
They are single‐valued functions on the 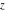 ‐plane cut along the interval ‐plane cut along the interval 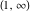 . They are continuous from below on the interval . They are continuous from below on the interval 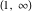 : :
For fixed  , the function , the function 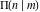 has two branch points at has two branch points at 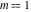 and and 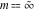 . For fixed . For fixed 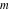 , the function , the function  has two branch points at has two branch points at 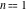 and and 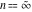 . .
Periodicity
All complete elliptic integrals 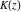 , , 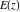 , and , and 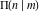 are not periodical functions. are not periodical functions.
Parity and symmetry
All complete elliptic integrals  , , 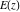 , and , and 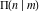 have mirror symmetry: have mirror symmetry:
Series representations
All complete elliptic integrals  , , 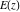 , and , and 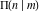 have the following series expansions at the point have the following series expansions at the point 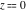 : :
The complete elliptic integrals 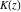 and and 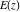 have the following series expansions at the point have the following series expansions at the point 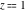 : :
The complete elliptic integrals 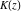 and and 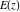 have the following series expansions at the point have the following series expansions at the point 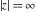 : :
The complete elliptic integral  has the following series expansions at the point has the following series expansions at the point 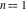 : :
The complete elliptic integral 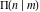 has the following series expansions at the point has the following series expansions at the point  : :
The complete elliptic integral 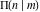 has the following series expansions at the point has the following series expansions at the point 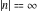 : :
The complete elliptic integral 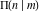 has the following series expansions at the point has the following series expansions at the point  : :
The previous formulas can be rewritten in summed forms of the truncated series expansion near corresponding points  , , 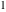 , or , or 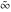 : :
Other series representations
Some elliptic integrals have special series representations through the elliptic nome  and inverse Jacobi elliptic functions by the formulas: and inverse Jacobi elliptic functions by the formulas:
Integral representations
The complete elliptic integrals  , , 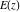 , and , and  have the following integral representations: have the following integral representations:
Identities
The complete elliptic integrals 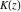 , ,  , and , and 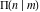 satisfy numerous identities, for example: satisfy numerous identities, for example:
Representations of derivatives
The first derivatives of all complete elliptic integrals 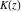 , , 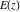 , and , and 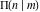 with respect to their variables can also be represented through complete elliptic integrals by the following formulas: with respect to their variables can also be represented through complete elliptic integrals by the following formulas:
The symbolic 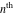 derivatives of all complete elliptic integrals derivatives of all complete elliptic integrals  , , 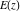 , and , and 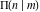 with respect to their variables can be represented through Gauss classical or regularized hypergeometric functions by the following formulas: with respect to their variables can be represented through Gauss classical or regularized hypergeometric functions by the following formulas:
Integration
The indefinite integrals of all complete elliptic integrals 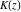 , , 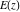 , and , and 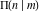 with respect to their variables can be expressed through complete elliptic integrals (or through hypergeometric functions of two variables) by the following formulas: with respect to their variables can be expressed through complete elliptic integrals (or through hypergeometric functions of two variables) by the following formulas:
Differential equations
All complete elliptic integrals 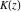 , ,  , and , and 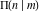 satisfy ordinary linear differential equations: satisfy ordinary linear differential equations:
Applications of complete elliptic integrals
Applications of complete elliptic integrals include geometry, physics, mechanics, electrodynamics, statistical mechanics, astronomy, geodesy, geodesics on conics, and magnetic field calculations.
|