|
General
Elliptic integrals were encountered in the work of J. Wallis (1655–1659) who investigated the integral in modern notation:
Broader interest in such integrals was stimulated by the appearance and development of integral calculus in the 18th and 19th centuries. Mathematicians found that integrals, containing quadratic polynomials under a square root of the form:
can be evaluated through elementary functions by formulas such as:
But these early mathematicians could not find simple formulas for similar integrals containing higher-degree polynomials:
Many important applications of these integrals were found at that time. The problem of evaluating such integrals was converted into the problem of evaluating only three basic integrals. They were later denoted by their special notation and named the incomplete elliptic integrals of the first, second, and third kinds—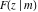 , , 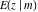 , and , and 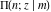 (A. M. Legendre): (A. M. Legendre):
The corresponding definite integrals (for 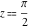 ) were named the complete elliptic integrals of the first, second, and third kinds denoted by the symbols ) were named the complete elliptic integrals of the first, second, and third kinds denoted by the symbols  , , 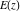 , and , and 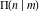 : :
These integrals were extensively studied for another important reason—development of the theory of the double periodic functions. These functions were called elliptic functions. The elliptic integrals and elliptic functions were studied simultaneously on several occasions throughout history and a deep connection exists between these two areas of mathematics. The following chronology reflects the main steps in building the theory of elliptic integrals.
L. Euler (1733, 1757, 1763, 1766) derived the addition theorem for the incomplete elliptic integrals 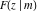 , and , and  . .
J.‐L. Lagrange (1783) and especially A. M. Legendre (1793, 1811, 1825–1828) devoted a lot of attention to the study of the different properties of those two elliptic integrals. C. F. Gauss (1799, 1818) also used these integrals during his research.
Simultaneously, A. M. Legendre (1811) introduced the incomplete elliptic integral of the third kind and the complete versions of all three elliptic integrals.
C. G. J. Jacobi (1827–1829) introduced inverse functons of the elliptic integrals 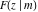 and and 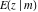 , which led him to build the theory of elliptic functions. In 1829, C. G. J. Jacobi defined the following function: , which led him to build the theory of elliptic functions. In 1829, C. G. J. Jacobi defined the following function:
which was later called the Jacobi zeta function. J. Liouville (1840) also studied elliptic integrals  and and 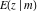 . .
N. H. Abel, independently from C. G. J. Jacobi, got some of his results and studied the so-called hyperelliptic and Abelian integrals.
|