|
All complete elliptic integrals 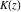 , ,  , and , and 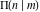 can be represented through more general functions.
Through the Gauss hypergeometric function: can be represented through more general functions.
Through the Gauss hypergeometric function:
Through the Meijer G function:
Through the hypergeometric Appell 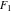 function of two variables: function of two variables:
Through the hypergeometric function of two variables:
Through the incomplete elliptic integrals:
Through the elliptic theta functions:
Through the arithmetic geometric mean:
Through the Jacobi elliptic functions:
Through the Weierstrass elliptic functions and inverse elliptic nome  : :
Through the Legendre 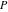 and and  functions: functions:
The complete elliptic integral 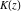 is related to Jacobi amplitude by the following formula, which demonstrates that Jacobi amplitude is the some kind of inverse function to the elliptic integral is related to Jacobi amplitude by the following formula, which demonstrates that Jacobi amplitude is the some kind of inverse function to the elliptic integral 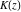 : :
All complete elliptic integrals 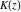 , , 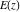 , and , and  can be represented through other complete elliptic integrals by the following formulas: can be represented through other complete elliptic integrals by the following formulas:
|