|
The incomplete elliptic integrals  , ,  , , 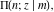 and and 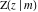 are equal to are equal to 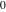 at the origin points: at the origin points:
The incomplete elliptic integrals 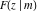 , ,  , , 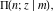 and and 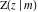 for particular argument values can be evaluated in closed forms, for example: for particular argument values can be evaluated in closed forms, for example:
At infinities, the incomplete elliptic integrals 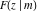 , , 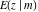 , , 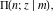 and and  have the following values: have the following values:
The incomplete elliptic integrals 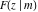 , , 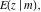 and and 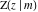 are analytical functions of are analytical functions of 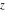 and and 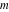 , which are defined over , which are defined over 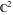 .
The incomplete elliptic integral .
The incomplete elliptic integral  is an analytical function of is an analytical function of 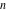 , , 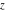 , and , and 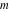 , which is defined over , which is defined over  . .
The incomplete elliptic integrals 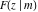 , ,  , , 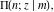 and and 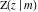 do not have poles and essential singularities with respect to their variables. do not have poles and essential singularities with respect to their variables.
For fixed 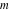 , the functions , the functions 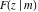 , , 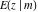 , and , and  have an infinite number of branch points at have an infinite number of branch points at 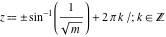 and and 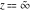 .
They have complicated branch cut. .
They have complicated branch cut.
For fixed 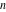 , , 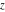 , the function , the function  has two branch points at has two branch points at 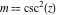 and and 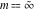 . For fixed . For fixed 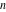 , ,  , the function , the function  has an infinite number of branch points at has an infinite number of branch points at 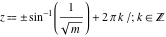 , , 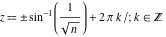 and and 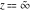 . For fixed . For fixed 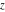 , ,  , the function , the function  does not have branch points. does not have branch points.
The incomplete elliptic integrals 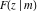 , ,  and and  are quasi‐periodic functions with respect to are quasi‐periodic functions with respect to 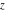 : :
The incomplete elliptic integral  is a periodic function with respect to is a periodic function with respect to 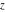 with period with period 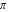 : :
The incomplete elliptic integrals 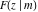 , ,  , , 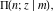 and and 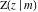 have mirror symmetry: have mirror symmetry:
The incomplete elliptic integrals 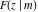 , , 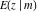 , ,  and and 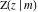 are odd functions with respect to are odd functions with respect to 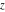 . .
The incomplete elliptic integral 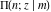 has the following series expansions at the point has the following series expansions at the point 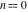 : :
The incomplete elliptic integrals 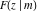 , , 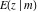 , , 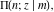 and and 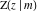 have the following series expansions at the point have the following series expansions at the point  : :
The incomplete elliptic integrals 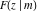 , , 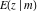 , , 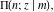 and and  have the following series expansions at the point have the following series expansions at the point  : :
The incomplete elliptic integrals 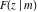 , , 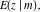 and and 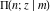 have the following series expansions at the point have the following series expansions at the point 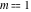 : :
The incomplete elliptic integrals 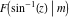 and and 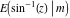 have the following series expansions at the point have the following series expansions at the point 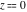 : :
The incomplete elliptic integrals 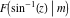 and and 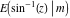 have the following series expansions at the point have the following series expansions at the point 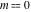 : :
The incomplete elliptic integrals 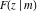 , , 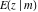 , , 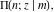 and and 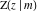 can be represented through different kinds of series, for example: can be represented through different kinds of series, for example:
where 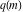 is an elliptic nome and is an elliptic nome and 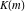 is a complete elliptic integral. is a complete elliptic integral.
The incomplete elliptic integrals 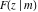 , ,  , , 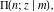 and and  have the following integral representations: have the following integral representations:
The incomplete elliptic integrals  , , 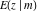 , , 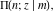 and and  with linear arguments can sometimes be simplified, for example: with linear arguments can sometimes be simplified, for example:
In some cases, simplification can be realized for more complicated arguments, for example:
Sums of the incomplete elliptic integrals 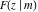 , , 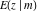 , , 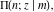 and and 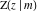 with different values with different values 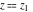 and and  can be evaluated by the following summation formulas: can be evaluated by the following summation formulas:
The incomplete elliptic integrals 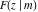 , ,  , , 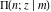 , and , and  satisfy numerous identities, for example: satisfy numerous identities, for example:
The first derivative of the incomplete elliptic integral 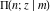 with respect to variable with respect to variable 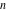 has the following representation: has the following representation:
The previous formula can be generalized to the 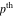 derivative: derivative:
The first derivatives of the incomplete elliptic integrals  , , 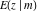 , , 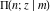 , and , and 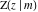 with respect to variable with respect to variable 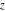 have the following simple representations: have the following simple representations:
The previous formulas can be generalized to the arbitrary-order symbolic derivatives:
The first derivatives of the incomplete elliptic integrals 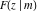 , ,  , , 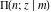 and and 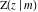 with respect to variable with respect to variable 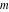 have the following representations: have the following representations:
The previous formulas can be generalized to the arbitrary-order symbolic derivatives:
The indefinite integral of the incomplete elliptic integral 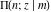 with respect to variable with respect to variable 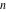 has the following representation through the infinite series that includes the Appell has the following representation through the infinite series that includes the Appell  hypergeometric function of two variables: hypergeometric function of two variables:
The indefinite integrals of all incomplete elliptic integrals 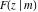 , , 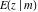 , ,  , and , and 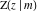 with respect to variable with respect to variable 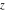 have the following representations: have the following representations:
The indefinite integrals of incomplete elliptic integrals 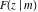 , , 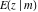 , and , and 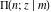 with respect to variable with respect to variable 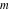 can be expressed in closed forms by the following formulas: can be expressed in closed forms by the following formulas:
The incomplete elliptic integrals 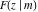 , , 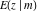 , , 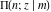 , and , and  satisfy the following differential equations: satisfy the following differential equations:
|