|
The exponential integral 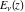 , exponential integral , exponential integral 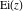 , logarithmic integral , logarithmic integral 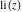 , sine integral , sine integral 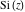 , hyperbolic sine integral , hyperbolic sine integral 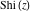 , cosine integral , cosine integral 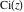 , and hyperbolic cosine integral , and hyperbolic cosine integral 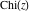 are defined as the following definite integrals, including the Euler gamma constant are defined as the following definite integrals, including the Euler gamma constant 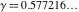 : :
The previous integrals are all interrelated and are called exponential integrals.
Instead of the above classical definitions through definite integrals, equivalent definitions through infinite series can be used, for example, the exponential integral 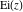 can be defined by the following formula (see the following sections for the corresponding series for the other integrals): can be defined by the following formula (see the following sections for the corresponding series for the other integrals):
|