|
The exponential integrals  , , 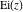 , , 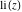 , , 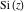 , , 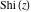 , , 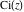 , and , and 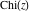 are the particular cases of the more general hypergeometric and Meijer G functions. are the particular cases of the more general hypergeometric and Meijer G functions.
For example, they can be represented through hypergeometric functions  or the Tricomi confluent hypergeometric function or the Tricomi confluent hypergeometric function 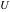 : :
Representations of the exponential integrals 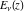 and and 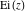 , the sine and cosine integrals , the sine and cosine integrals 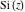 and and  , and the hyperbolic sine and cosine integrals , and the hyperbolic sine and cosine integrals 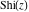 and and 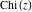 through classical Meijer G functions are rather simple: through classical Meijer G functions are rather simple:
Here 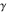 is the Euler gamma constant is the Euler gamma constant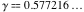 and the complicated‐looking expression containing the two logarithm simplifies piecewise: and the complicated‐looking expression containing the two logarithm simplifies piecewise:
But the last four formulas that contain the Meijer G function can be simplified further by changing the classical Meijer 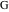 functions to the generalized one. These formulas do not include factors functions to the generalized one. These formulas do not include factors 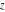 and terms and terms 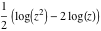 : :
The corresponding representations of the logarithmic integral 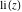 through the classical Meijer G function is more complicated and includes composition of the G function and a logarithmic function: through the classical Meijer G function is more complicated and includes composition of the G function and a logarithmic function:
All six exponential integrals of one variable are the particular cases of the incomplete gamma function:
The exponential integral 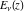 can be represented through the incomplete gamma function or the regularized incomplete gamma function: can be represented through the incomplete gamma function or the regularized incomplete gamma function:
The exponential integral 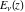 is connected with the inverse of the regularized incomplete gamma function is connected with the inverse of the regularized incomplete gamma function 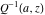 by the following formula: by the following formula:
The exponential integrals 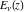 , , 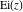 , , 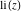 , , 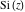 , , 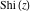 , ,  , and , and  are interconnected through the following formulas: are interconnected through the following formulas:
|