|
The exponential‐type integrals have a long history. After the early developments of differential calculus, mathematicians tried to evaluate integrals containing simple elementary functions, especially integrals that often appeared during investigations of physical problems. Despite the relatively simple form of the integrands, some of these integrals could not be evaluated through known functions. Examples of integrals that could not be evaluated in known functions are:

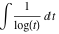
|

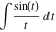
|

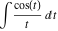
|


|
L. Euler (1768) introduced the first integral shown in the preceding list. Later L. Mascheroni (1790, 1819) used it and introduced the second and third integrals, and A. M. Legendre (1811) introduced the last integral shown. T. Caluso (1805) used the first integral in an article and J. von Soldner (1809) introduced its notation through symbol li. F. W. Bessel (1812) used the second and third integrals. C. A. Bretschneider (1843) not only used the second and third integrals, but also introduced similar integrals for the hyperbolic functions:
O. Schlömilch (1846) and F. Arndt (1847) widely used such integrals containing the exponential and trigonometric functions. For the exponential, sine, and cosine integrals, J. W. L. Glaisher (1870) introduced the notations 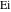 , , 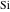 , and , and 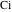 . H. Amstein (1895) introduced the branch cut for the logarithmic integral with a complex argument. N. Nielsen (1904) used the notations . H. Amstein (1895) introduced the branch cut for the logarithmic integral with a complex argument. N. Nielsen (1904) used the notations 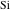 and and 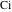 for corresponding integrals. for corresponding integrals.
Different notations are used for the previous definite integrals by various authors when they are integrated from 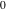 to to 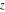 or from or from  to to  . .
|