|
Introduction to the probability integrals and inverses
General
The probability integral (error function) 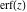 has a long history beginning with the articles of A. de Moivre (1718–1733) and P.‐S. Laplace (1774) where it was expressed through the following integral: has a long history beginning with the articles of A. de Moivre (1718–1733) and P.‐S. Laplace (1774) where it was expressed through the following integral:
Later C. Kramp (1799) used this integral for the definition of the complementary error function 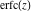 . P.‐S. Laplace (1812) derived an asymptotic expansion of the error function. . P.‐S. Laplace (1812) derived an asymptotic expansion of the error function.
The probability integrals were so named because they are widely applied in the theory of probability, in both normal and limit distributions.
To obtain, say, a normal distributed random variable from a uniformly distributed random variable, the inverse of the error function, namely 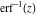 is needed. The inverse was systematically investigated in the second half of the twentieth century, especially by J. R. Philip (1960) and A. J. Strecok (1968). is needed. The inverse was systematically investigated in the second half of the twentieth century, especially by J. R. Philip (1960) and A. J. Strecok (1968).
Definitions of probability integrals and inverses
The probability integral (error function) 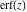 , the generalized error function , the generalized error function  , the complementary error function , the complementary error function 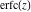 , the imaginary error function , the imaginary error function 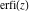 , the inverse error function , the inverse error function 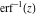 , the inverse of the generalized error function , the inverse of the generalized error function 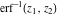 , and the inverse complementary error function , and the inverse complementary error function 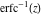 are defined through the following formulas: are defined through the following formulas:
These seven functions are typically called probability integrals and their inverses.
Instead of using definite integrals, the three univariate error functions can be defined through the following infinite series.
A quick look at the probability integrals and inverses Here is a quick look at the graphics for the probability integrals and inverses along the real axis.
Connections within the group of probability integrals and inverses and with other function groups
Representations through more general functions
The probability integrals  , , 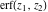 , ,  , and , and 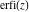 are the particular cases of two more general functions: hypergeometric and Meijer G functions. are the particular cases of two more general functions: hypergeometric and Meijer G functions.
For example, they can be represented through the confluent hypergeometric functions 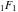 and and 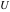 : :
Representations of the probability integrals 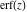 , , 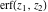 , , 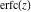 , and , and 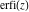 through classical Meijer G functions are rather simple: through classical Meijer G functions are rather simple:
The factor 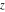 in the last four formulas can be removed by changing the classical Meijer G functions to the generalized one: in the last four formulas can be removed by changing the classical Meijer G functions to the generalized one:
The probability integrals 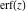 , , 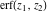 , ,  , and , and 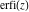 are the particular cases of the incomplete gamma function, regularized incomplete gamma function, and exponential integral are the particular cases of the incomplete gamma function, regularized incomplete gamma function, and exponential integral  : :
Representations through related equivalent functions
The probability integrals 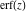 , , 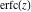 , and , and 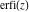 can be represented through Fresnel integrals by the following formulas: can be represented through Fresnel integrals by the following formulas:
Representations through other probability integrals and inverses
The probability integrals and their inverses 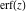 , , 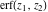 , , 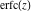 , , 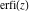 , , 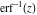 , , 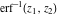 , and , and 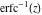 are interconnected by the following formulas: are interconnected by the following formulas:
The best-known properties and formulas for probability integrals and inverses
Real values for real arguments
For real values of argument  , the values of the probability integrals , the values of the probability integrals 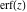 , , 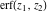 , , 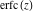 , and , and 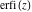 are real. For real arguments are real. For real arguments 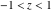 , the values of the inverse error function , the values of the inverse error function 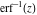 are real; for real arguments are real; for real arguments 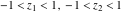 , the values of the inverse of the generalized error function , the values of the inverse of the generalized error function 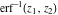 are real; and for real arguments are real; and for real arguments 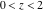 , the values of the inverse complementary error function , the values of the inverse complementary error function 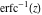 are real. are real.
Simple values at zero and one
The probability integrals 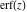 , ,  , , 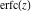 , and , and 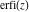 , and their inverses , and their inverses 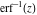 , , 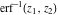 , and , and  have simple values for zero or unit arguments: have simple values for zero or unit arguments:
Simple values at infinity
The probability integrals  , , 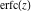 , and , and  have simple values at infinity: have simple values at infinity:
Specific values for specialized arguments
In cases when  or or 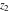 is equal to is equal to 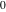 or or 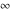 , the generalized error function , the generalized error function 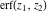 and its inverse and its inverse 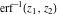 can be expressed through the probability integrals can be expressed through the probability integrals  , , 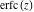 , or their inverses by the following formulas: , or their inverses by the following formulas:
Analyticity
The probability integrals 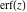 , , 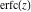 , and , and 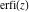 , and their inverses , and their inverses 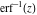 , and , and 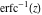 are defined for all complex values of are defined for all complex values of 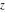 , and they are analytical functions of , and they are analytical functions of  over the whole complex over the whole complex 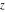 ‐plane. The probability integrals ‐plane. The probability integrals 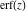 , , 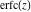 , and , and 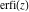 are entire functions with an essential singular point at are entire functions with an essential singular point at 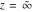 , and they do not have branch cuts or branch points. , and they do not have branch cuts or branch points.
The generalized error function 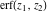 is an analytical function of is an analytical function of 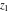 and and 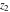 , which is defined in , which is defined in  . For fixed . For fixed 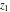 , it is an entire function of , it is an entire function of  . For fixed . For fixed 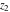 , it is an entire function of , it is an entire function of 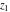 . It does not have branch cuts or branch points.
The inverse of the generalized error function . It does not have branch cuts or branch points.
The inverse of the generalized error function  is an analytical function of is an analytical function of 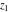 and and 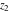 , which is defined in , which is defined in 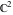 . .
Poles and essential singularities
The probability integrals 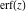 , , 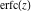 , and , and 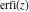 have only one singular point at have only one singular point at 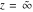 . It is an essential singular point. . It is an essential singular point.
The generalized error function 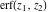 has singular points at has singular points at 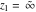 and and 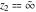 . They are essential singular points. . They are essential singular points.
Periodicity
The probability integrals 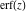 , , 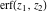 , ,  , and , and 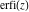 , and their inverses , and their inverses 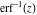 , , 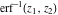 , and , and 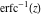 do not have periodicity. do not have periodicity.
Parity and symmetry
The probability integrals 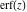 , , 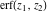 , and , and 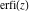 are odd functions and have mirror symmetry: are odd functions and have mirror symmetry:
The generalized error function 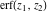 has permutation symmetry: has permutation symmetry:
The complementary error function 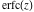 has mirror symmetry: has mirror symmetry:
Series representations
The probability integrals 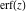 , , 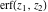 , , 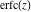 , and , and 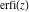 , and their inverses , and their inverses 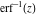 and and 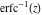 have the following series expansions: have the following series expansions:
The series for functions 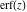 , , 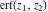 , , 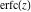 , and , and 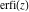 converge for all complex values of their arguments. converge for all complex values of their arguments.
Interestingly, closed-form expressions for the truncated version of the Taylor series at the origin can be expressed through generalized hypergeometric function 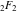 , for example: , for example:
Asymptotic series expansions
The asymptotic behavior of the probability integrals 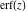 , , 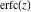 , and , and 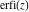 can be described by the following formulas (only the main terms of the asymptotic expansion are given): can be described by the following formulas (only the main terms of the asymptotic expansion are given):
The previous formulas are valid in any direction approaching infinity (z∞). In particular cases, these formulas can be simplified to the following relations:
Integral representations
The probability integrals 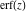 , , 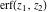 , ,  , and , and  can also be represented through the following equivalent integrals: can also be represented through the following equivalent integrals:
The symbol 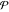 in the preceding integral means that the integral evaluates as the Cauchy principal value: in the preceding integral means that the integral evaluates as the Cauchy principal value: 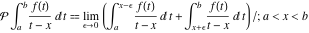 . .
Transformations
If the arguments of the probability integrals 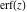 , , 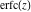 , and , and 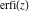 contain square roots, the arguments can sometimes be simplified: contain square roots, the arguments can sometimes be simplified:
Representations of derivatives
The derivative of the probability integrals 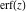 , , 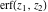 , , 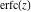 , and , and 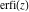 , and their inverses , and their inverses 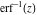 , ,  , and , and 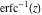 have simple representations through elementary functions: have simple representations through elementary functions:
The symbolic 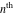 -order derivatives from the probability integrals -order derivatives from the probability integrals 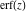 , , 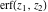 , , 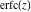 , and , and 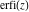 have the following simple representations through the regularized generalized hypergeometric function have the following simple representations through the regularized generalized hypergeometric function 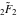 : :
But the symbolic 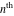 -order derivatives from the inverse probability integrals -order derivatives from the inverse probability integrals 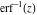 , ,  , and , and 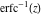 have very complicated structures in which the regularized generalized hypergeometric function have very complicated structures in which the regularized generalized hypergeometric function 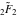 appears in the multidimensional sums, for example: appears in the multidimensional sums, for example:
Differential equations
The probability integrals 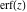 , ,  , , 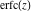 , and , and 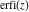 satisfy the following second-order linear differential equations: satisfy the following second-order linear differential equations:
where 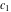 and and 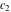 are arbitrary constants. are arbitrary constants.
The inverses of the probability integrals  , , 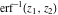 , and , and  satisfy the following ordinary second-order nonlinear differential equations: satisfy the following ordinary second-order nonlinear differential equations:
Applications of probability integrals and inverses
Applications of probability integrals include solutions of linear partial differential equations, probability theory, Monte Carlo simulations, and the Ewald method for calculating electrostatic lattice constants.
|